Đề1Cho HF // MD , F = 140 độ , D = 155 độ Tính FED
Đề2Cho hình vẽ biết A = 40 độ C = 35 độ và ABC bằng 75 độ chứng minh AH // CM
[Mình không kịp vẽ hình nếu rảnh thì các bạn vẽ giúp mình nha còn không thì giải thôi ]
Mình cảm mơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: BC=25cm
b: Xét ΔBAC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{3}=\dfrac{CD}{5}=\dfrac{AD+CD}{3+5}=\dfrac{20}{8}=2.5\)
Do đó: AD=7,5cm; CD=12,5(cm)
b: \(AH=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
\(HB=\dfrac{15^2}{25}=9\left(cm\right)\)
c: góc AID=góc BIH=90 độ-góc DBC
góc ADI=90 độ-góc ABD
mà góc ABD=góc DBC
nên góc ADI=góc AID
hay ΔAID cân tại A

Bạn có thể vẽ ra tập rồi trả lời câu hỏi mới dễ bạn à.
Còn trên đây mk ko biết vẽ hình.
Hoặc bạn có thể vào học 24 hoặc câu hỏi tương tự tham khảo.
Chúc bạn học tốt !

( Hình minh họa cho cả 3 câu :> )
a, Ta có: \(\widehat{O_1}=\widehat{O_3}\)( 2 góc đối đỉnh )
Mà \(\widehat{O_1}=75^o\)
\(\Rightarrow\widehat{O_3}=75^o\)
Lại có: \(\widehat{O_1}+\widehat{O_2}=180^o\)( 2 góc kề bù )
\(\Rightarrow75^o+\widehat{O_2}=180^o\)
\(\Rightarrow\widehat{O_2}=105^o\)
Mà \(\widehat{O_2}=\widehat{O_4}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{O_4}=105^o\)
b, Ta có: \(\widehat{O_1}+\widehat{O_3}=180^o\)
Mà \(\widehat{O_1}=\widehat{O_3}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{O_1}=\widehat{O_3}=90^o\)
Lại có: \(\widehat{O_1}+\widehat{O_2}=180^o\)( 2 gkb )
\(\Rightarrow\widehat{O_2}=90^o\)
Mà \(\widehat{O_2}=\widehat{O_4}\)( 2 góc đối đỉnh )
\(\Rightarrow\widehat{O_4}=90^o\)
c, Ta có: \(\widehat{O_1}+\widehat{O_2}=180^o\)
Mà \(\widehat{O_2}-\widehat{O_1}=30^o\)
\(\Rightarrow\widehat{O_1}=\frac{\left(180^o-30^o\right)}{2}=75^o\)
\(\Rightarrow\widehat{O_2}=180-75^o=105^o\)
Mà \(\widehat{O_1}=\widehat{O_3}=75^o\)
\(\widehat{O_2}=\widehat{O_4}=105^o\)
P/s: Sai thì thông cảm :(
Giải: Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\) (kề bù)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-75^0=105^0\)
Ta lại có: +) \(\widehat{O_1}=\widehat{O_3}\) (đối đỉnh)
Mà \(\widehat{O_1}=75^0\) => \(\widehat{O_3}=75^0\)
+) \(\widehat{O_2}=\widehat{O_4}\)(đối đỉnh)
Mà \(\widehat{O_2}=105^0\) => \(\widehat{O_4}=105^0\)
b) Ta có: \(\widehat{O_1}+\widehat{O_3}=140^0\)
Mà \(\widehat{O_1}=\widehat{O_3}\)(đối đỉnh)
=> \(\widehat{O_1}=\widehat{O_3}=\frac{140^0}{2}=70^0\)
Ta lại có: \(\widehat{O_1}+\widehat{O_2}=180^0\)(kề bù)
=> \(\widehat{O_2}=180^0-\widehat{O_1}=180^0-70^0=110^0\)
=> \(\widehat{O_2}=\widehat{O_4}=110^0\)(đối đỉnh)
c) Ta có: \(\widehat{O_1}+\widehat{O_2}=180^0\)(kề bù)
Mà \(\widehat{O_2}-\widehat{O_1}=30^0\)
=> \(2.\widehat{O_2}=180^0+30^0=210^0\)
=> \(\widehat{O_2}=210^0:2=105^0\)
=> \(\widehat{O_1}=180^0-105^0=75^0\)
Ta lại có: \(\widehat{O_1}=\widehat{O_3}\) (đối đỉnh)
Mà \(\widehat{O_1}=75^0\) => \(\widehat{O_3}=75^0\)
+) \(\widehat{O_2}=\widehat{O_4}\) (đối đỉnh)
Mà \(\widehat{O_2}=105^0\) => \(\widehat{O_4}=105^0\)
(hình chắc đúng, từng làm qua)

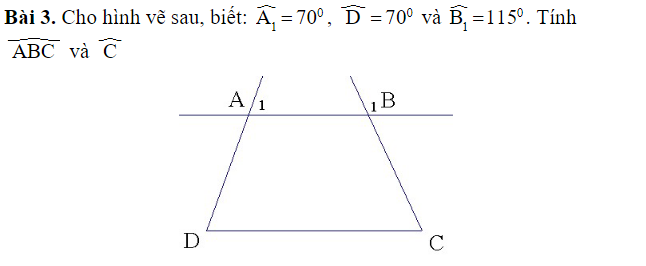
Do góc A1= góc D mà hai góc này là cặp góc đồng vị
-> AB // CD
Ta có góc ABC là góc đối đỉnh của góc B1 nên:
-> góc B1= góc ABC -> góc ABC = 115 độ
Do AB // CD nên tổng hai góc trong cùng phía bằng 180 độ
-> góc ABC + góc C = 180 độ -> góc C = 180 độ - 115 độ = 65 độ

Ta có: \(\widehat{ABC}=\widehat{B_1}=115^0\)(đối đỉnh)
Ta có: \(\widehat{A_1}=\widehat{D}=70^0\)
Mà 2 góc này so le trong
=> AB//CD
\(\Rightarrow\widehat{ABC}+\widehat{C}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{C}=180^0-115^0=65^0\)
Do góc A1= góc D mà hai góc này là cặp góc đồng vị
-> AB // CD
Ta có góc ABC là góc đối đỉnh của góc B1 nên:
-> góc B1= góc ABC -> góc ABC = 115 độ
Do AB // CD nên tổng hai góc trong cùng phía bằng 180 độ
-> góc ABC + góc C = 180 độ -> góc C = 180 độ - 115 độ = 65 độ
Không có hình không làm được em ơi