1) Cho phương trình: \(x^2+\frac{1}{x^2}+4\left(x+\frac{1}{x}\right)-3-2m=0\). Tìm m để phương trình có nghiệm.
2) Cho phương trình: \(x^2-2x+3-\left(m+1\right)\sqrt{x^2-2x+5}-m=0\). Tìm m để phương trình có nghiệm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 5 2016
\(\Leftrightarrow2m.2^x+\left(2m+1\right)\left(3-\sqrt{5}\right)^x+\left(3+\sqrt{5}\right)^x=0\)
\(\Leftrightarrow\left(\frac{3+\sqrt{5}}{2}\right)^x+\left(2m+1\right)\left(\frac{3-\sqrt{5}}{2}\right)^x+2m< 0\)
Đặt \(t=\left(\frac{3+\sqrt{5}}{2}\right)^x,0< t\le1\Rightarrow\frac{1}{t}=\left(\frac{3-\sqrt{5}}{2}\right)^x\)
Phương trình trở thành :
\(t+\left(2m+1\right)\frac{1}{t}+2m=0\) (*)
a. Khi \(m=-\frac{1}{2}\) ta có \(t=1\) suy ra \(\left(\frac{3+\sqrt{5}}{2}\right)^x=1\Leftrightarrow x=0\)
Vậy phương trình có nghiệm là \(x=0\)
b. Phương trình (*) \(\Leftrightarrow t^2+1=-2m\left(t+1\right)\Leftrightarrow\frac{t^2+1}{t+1}=-2m\)
Xét hàm số \(f\left(t\right)=\frac{t^2+1}{t+1};t\in\)(0;1]
Ta có : \(f'\left(t\right)=\frac{t^2+2t+1}{\left(t+1\right)^2}\Rightarrow f'\left(t\right)=0\Leftrightarrow=-1+\sqrt{2}\)
Suy ra phương trình đã cho có nghiệm đúng
\(\Leftrightarrow2\sqrt{2}-2\le-2m\le1\Leftrightarrow\sqrt{2}-1\ge m\ge-\frac{1}{2}\)
Vậy \(m\in\left[-\frac{1}{2};\sqrt{2}-1\right]\) là giá trị cần tìm
30 tháng 7 2021
b) Thay x=2 vào pt, ta được:
\(4\left(m^2-1\right)-4m+m^2+m+4=0\)
\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)
\(\Leftrightarrow5m^2-3m=0\)
\(\Leftrightarrow m\left(5m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=\dfrac{2m}{m^2-1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)
5 tháng 1 2022
a: \(\Leftrightarrow\left(2m+1\right)^2-4\left(m^2-3\right)=0\)
\(\Leftrightarrow4m^2+4m+1-4m^2+12=0\)
=>4m=-13
hay m=-13/4
c: \(\Leftrightarrow\left(2m-2\right)^2-4m^2>=0\)
\(\Leftrightarrow4m^2-8m+4-4m^2>=0\)
=>-8m>=-4
hay m<=1/2
18 tháng 4 2023
1:
\(=\left(\dfrac{1}{x-2\sqrt{x}}+\dfrac{2}{3\sqrt{x}-6}\right):\dfrac{2\sqrt{x}+3}{3\sqrt{x}}\)
\(=\dfrac{3+2\sqrt{x}}{3\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{3\sqrt{x}}{2\sqrt{x}+3}=\dfrac{1}{\sqrt{x}-2}\)
11 tháng 3 2022
PT có nghiệm $x_1=2$
\(\Leftrightarrow4-6\left(m-1\right)+2m-4=0\\ \Leftrightarrow6-4m=0\Leftrightarrow m=\dfrac{3}{2}\)
Theo Vi-ét: \(x_1+x_2=3\left(m-1\right)=\dfrac{3}{2}\)
\(\Leftrightarrow2+x_2=\dfrac{3}{2}\Leftrightarrow x_2=-\dfrac{1}{2}\)
Vậy nghiệm còn lại là $-\frac{1}{2}$
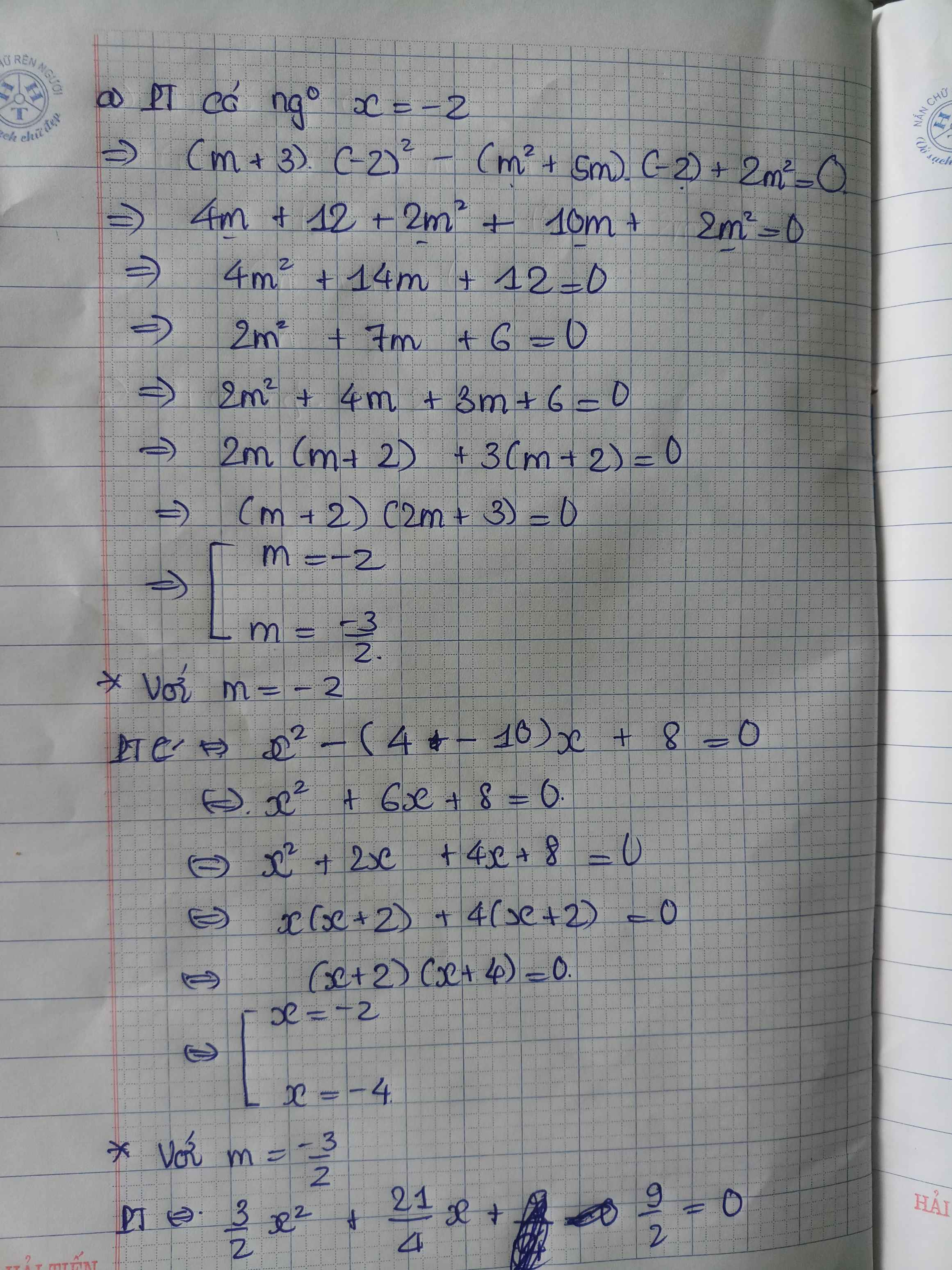
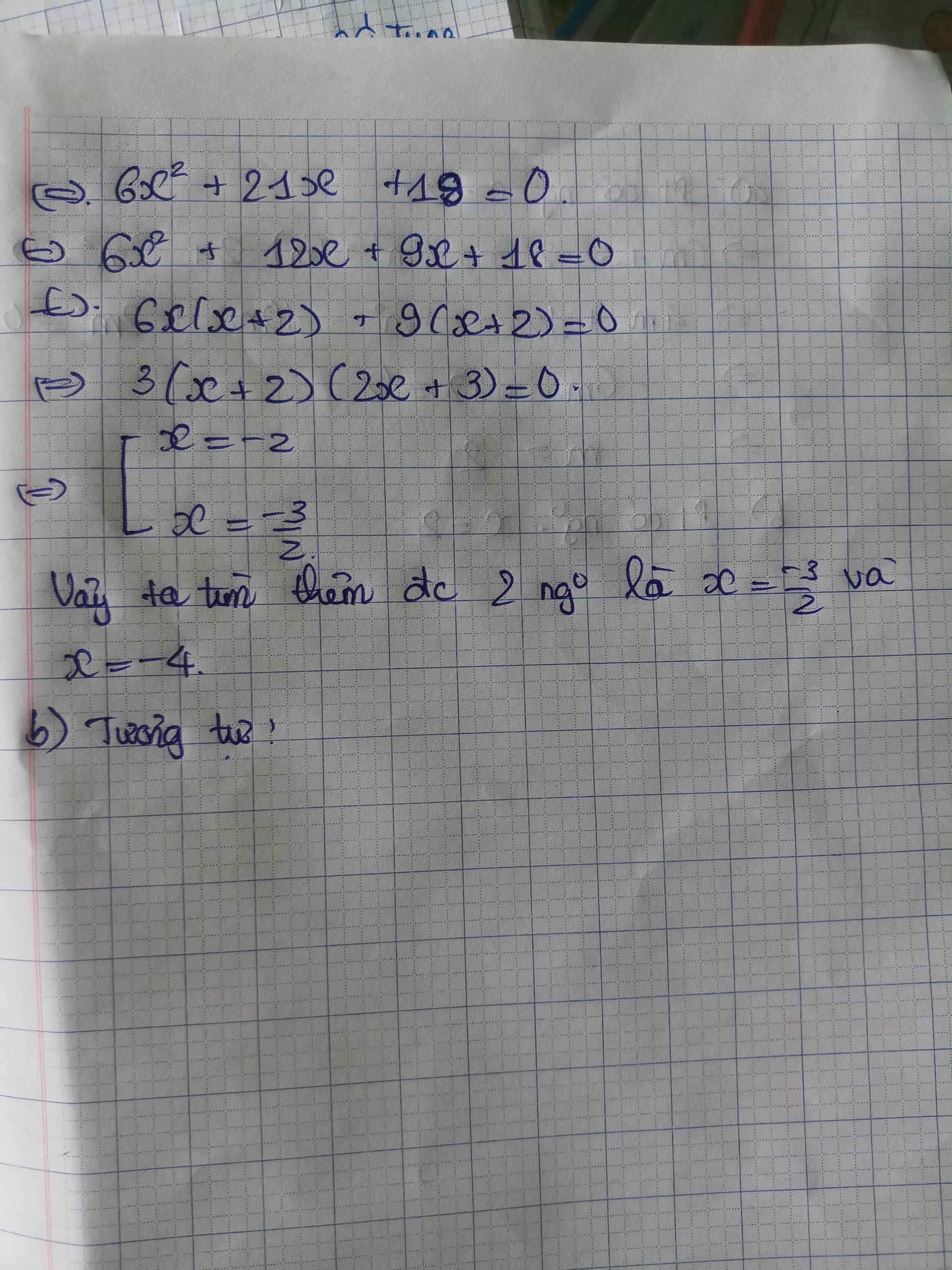
@Akai Haruma @Nguyễn Việt Lâm
cíu giúp em với ạaaa
1.
Đặt \(x+\frac{1}{x}=t\Rightarrow\left|t\right|\ge2\)
Pt trở thành: \(t^2-2+4t-3-2m=0\)
\(\Leftrightarrow t^2+4t-5=2m\)
Xét \(f\left(t\right)=t^2+4t-5\) trên \((-\infty;-2]\cup[2;+\infty)\)
\(-\frac{b}{2a}=-2\) ; \(f\left(-2\right)=-9\) ; \(f\left(2\right)=7\)
\(\Rightarrow f\left(x\right)\ge-9\Rightarrow\) pt có nghiệm khi và chỉ khi \(2m\ge-9\Leftrightarrow m\ge-\frac{9}{2}\)
2.
Đặt \(\sqrt{x^2-2x+5}=\sqrt{\left(x-1\right)^2+4}=t\Rightarrow t\ge2\)
\(t^2-2-\left(m+1\right)t-m=0\)
\(\Leftrightarrow t^2-t-2-m\left(t+1\right)=0\)
\(\Leftrightarrow\left(t+1\right)\left(t-2\right)-m\left(t+1\right)=0\)
\(\Leftrightarrow\left(t+1\right)\left(t-m-2\right)=0\)
\(\Leftrightarrow m=t+2\ge4\)
Vậy \(m\ge4\) thì pt có nghiệm