cho x,y thuộc z cm a=(x-y)(x-2y(x-3y)(x-4y)+y^4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(B=x\left(x+y\right)\left(x-y\right)\left(x+2y\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+2xy-xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)^2-2y^2\left(x^2+xy\right)+y^4\)
\(=\left(x^2+xy-y^2\right)^2\)
b: \(C=\left(x-y\right)\left(x-4y\right)\left(x-2y\right)\left(x-3y\right)+y^4\)
\(=\left(x^2-5xy+4y^2\right)\left(x^2-5xy+6y^2\right)+y^4\)
\(=\left(x^2-5xy\right)^2+10y^2\left(x^2-5xy\right)+25y^4\)
\(=\left(x^2-5xy+5y^2\right)^2\)

A=\([\)(x+y)(x+4y)\(][\)(x+2y)(x+3y)]+y4
=(x2+4xy+xy+4y2)(x2+3xy+2xy+6y2)+y4
=(x2+5xy+4y2)(x2+5xy+6y2)+y4
=(x2+5xy+5y2-y2)(x2+5xy+5y2+y2)+y4
=(x2+5xy+5y2)2-y4+y4
=(x2+5xy+5y2)2
vậy A là số chính phương vs \(\forall\) x,y\(\in\)R

N = ( x - y )( x - 2y )( x - 3y )( x - 4y ) + y4
= [ ( x - y )( x - 4y ) ][ ( x - 2y )( x - 3y ) ] + y4
= ( x2 - 5xy + 4y2 )( x2 - 5xy + 6y2 ) + y4
Đặt t = x2 - 5xy + 5y2
N = ( t - y2 )( t + y2 ) + y4
= t2 - y4 + y4
= t2 = ( x2 - 5xy + 5y2 )2
Vì x, y thuộc Z => x2 thuộc Z ; -5xy thuộc Z ; 5y2 thuộc Z
=> ( x2 - 5xy + 5y2 )2 là một số chính phương
=> đpcm
\(N=\left(x-y\right)\left(x-2y\right)\left(x-3y\right)\left(x-4y\right)+y^4\)
\(=\left(x-y\right)\left(x-4y\right)\left(x-2y\right)\left(x-3y\right)+y^4\)
\(=\left(x^2-5xy+4y^2\right)\left(x^2-5xy+6y^2\right)+y^4\)
Đặt \(x^2-5xy+5y^2=t\)
\(\Rightarrow\left(t-y^2\right)\left(t+y^2\right)+y^4=t^2-y^4+y^4=t^2\)
\(=\left(x^2-5xy+5y^2\right)^2\)
Vì \(x,y\inℤ\)\(\Rightarrow\left(x^2-5xy+5y^2\right)^2\)là số chính phương
hay \(N=\left(x-y\right)\left(x-2y\right)\left(x-3y\right)\left(x-4y\right)+y^4\)là số chính phương ( đpcm )

Mình làm một câu để bạn tham khảo, sau đó bạn áp dụng làm các bài còn lại nha ^^
Có gì không hiểu bạn ib nha ^^
1. \(2x=3y-2x\left(1\right)\) và \(x+y=14\)
\(\left(1\right)\Leftrightarrow4x=3y\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{4}\)
Theo tính chất dãy tỉ số bằng nhau, có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{14}{7}=2\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2.3=6\\y=2.4=8\end{matrix}\right.\)
Bạn tự kết luận ^^
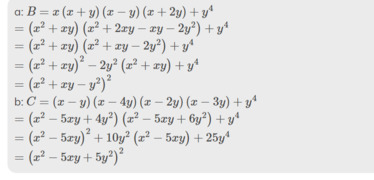
CM a là số chính phương, đề như thế này
Ta có:
\(a=\left(x-y\right)\left(x-2y\right)\left(x-3y\right)\left(x-4y\right)+y^4\)
\(a=\left[\left(x-y\right)\left(x-4y\right)\right]\left[\left(x-2y\right)\left(x-3y\right)\right]+y^4\)
\(a=\left(x^2-5xy+4y^2\right)\left(x^2-5xy+6y^2\right)+y^4\)
\(a=\left[\left(x^2-5xy+5y^2\right)-y^2\right]\left[\left(x^2-5xy+5y^2\right)+y^2\right]+y^4\)
\(a=\left(x^2-5xy+5y^2\right)^2-y^4+y^4\)
\(a=\left(x^2-5xy+5y^2\right)^2\) là SCP
=>đpcm
Chứng minh là một SCP chứ gì (:
A = ( x - y )( x - 2y )( x - 3y )( x - 4y ) + y4
= [ ( x - y )( x - 4y ) ][ ( x - 2y )( x - 3y ) ] + y4
= ( x2 - 5xy + 4y2 )( x2 - 5xy + 6y2 ) + y4 (1)
Đặt t = x2 - 5xy + 5y2
(1) <=> ( t - y2 )( t + y2 ) + y4
= t2 - y4 + y4
= t2 = ( x2 - 5xy + 5y2 )2
Vì x, y ∈ Z => x2 ∈ Z , -5xy ∈ Z , 5y2 ∈ Z
=> ( x2 - 5xy + 5y2 )2 là một SCP
=> đpcm