Hai địa điểm A và B cách nhau 300m. Khi vật thứ nhất qua A với vận tốc 20 m/s thì chuyển động chậm dần đều về phía B với gia tốc 1 m/s2. Cùng thời điểm, vật thứ hai bắt đầu chuyển động đều từ B về A với vận tốc 8 m/s. Chọn gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc vật thứ nhất qua A.
a) Viết phương trình tọa độ của hai vật.
b) Khi hai vật gặp nhau thì vật...
Đọc tiếp
Hai địa điểm A và B cách nhau 300m. Khi vật thứ nhất qua A với vận tốc 20 m/s thì chuyển động chậm dần đều về phía B với gia tốc 1 m/s2. Cùng thời điểm, vật thứ hai bắt đầu chuyển động đều từ B về A với vận tốc 8 m/s. Chọn gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc vật thứ nhất qua A.
a) Viết phương trình tọa độ của hai vật.
b) Khi hai vật gặp nhau thì vật thứ nhất còn chuyển động không? Xác định thời điểm và vị trí gặp nhau.
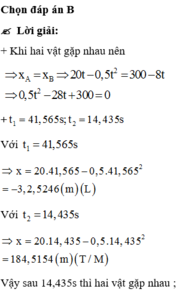
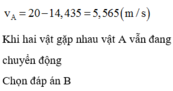
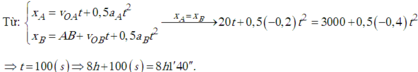
a) Phương trình chuyển động của hai vật: \(\left\{{}\begin{matrix}x_1=20t-\frac{1}{2}t^2\left(m\right)\\x_2=300-8t\left(m\right)\end{matrix}\right.\)
b) Phương trình vận tốc của vật 1: v1 = 20 - t (m/s)
Khi vật 1 dừng lại: v1 = 0 <=> 20 - t1 = 0
=> t1 = 20s
Hai vật gặp nhau khi:
x1 = x2 <=> 20t - \(\frac{1}{2}t^2=300-8t\Leftrightarrow\left\{{}\begin{matrix}t=41,56s\\t=14,44s\end{matrix}\right.\)
Với
t = 41,56s ta có: x1 = \(2.41,56-\frac{1}{2}.41,56^2=-32,4168\left(m\right)\)(loại vì vật 1 xuất phát từ gốc tọa độ và đi theo chiều dương)
Với t = 14,44s ta có: x1 = \(20.14,44-\frac{1}{2}.14,44^2=184,54\left(m\right)\)
t < t1 => khi hai vật gặp nhau, vật 1 vẫn chuyển động
Vậy hai xe gặp nhau sau 14,44s kể từ khi xuất phát tại vị trí cách điểm xuất phát của vật 1 một khoảng 184,54(m)