chỉ ra các cặp x y thỏa mãn |x2+2x| + |y2-9| = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
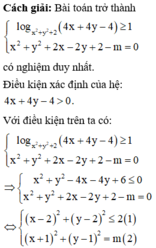


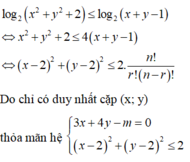
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
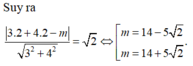
Chọn C.

log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B

\(x^2+2x+y^2-9=0\)
\(\Leftrightarrow\left(x+1\right)^2+y^2=10\)
Ta thấy VT là tổng 2 số chính phương nên ta tách VT thành tổng 2 số chính phương
Mà ta có: 10 = 1 + 9 = 9 + 1
\(\Rightarrow\)((x + 1)2, y2) = (1, 9; 9, 1)
Thế vào giải tiếp sẽ ra

Vì \(\left|x^2+2x\right|\ge0\) và \(\left|y^2-9\right|\ge0\)
=> Dấu = xảy ra khi : \(\hept{\begin{cases}x^2-2x=0\\y^2-9=0\end{cases}}\) => \(\hept{\begin{cases}x\left(x+2\right)=0\\\left(y-3\right)\left(y+3\right)=0\end{cases}}\) => \(\hept{\begin{cases}x=\left\{0;2\right\}\\y=\left\{3;-3\right\}\end{cases}}\)




b)|x^2+2x| + |y^2-9| = 0
 x^2+2x=0 và y^2-9=0
x^2+2x=0 và y^2-9=0
|x^2+2x| > hoặc =0
|y^2-9| > hoặc =0
suy ra (x;y)=(0;3)(0;-3)(-2;3)(-2;-3)
bài này lớp 6 như em làm được