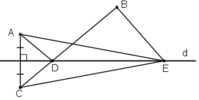
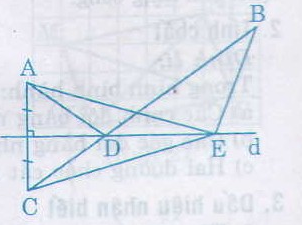
Bài 1. Cho đường thẳng d, 2 điểm A và B nằm cùng ở một mặt phẳng có bờ là đường thẳng d ( A,B không thuộc d). Gọi C và D thứ tự là điểm đối xứng của A,B qua đường thẳng d.
a. Chứng minh tứ giác ABCD là hình thang cân
b. Gọi E là giao điểm của BC và đường thẳng d, F thuộc đường thẳng d, F khác E. Chứng minh BF+FC>BE+EA
c. 1 người đi từ A đến d rồi lại về B. Hỏi đi qua đường nào là ngắn nhất