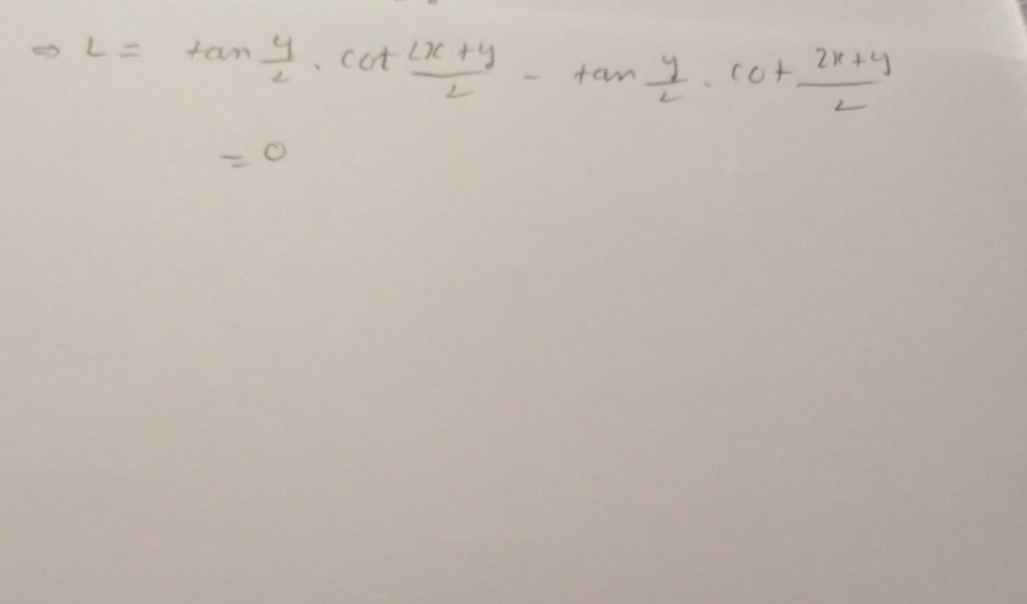A = cos(x+y)+cos(x-y) / cos(x+y) cos(x-y)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 7 2021
a.
\(y=\dfrac{3}{2}sin2x-2\left(cos^2x-sin^2x\right)+5=\dfrac{3}{2}sin2x-2cos2x+5\)
\(=\dfrac{5}{2}\left(\dfrac{3}{5}sin2x-\dfrac{4}{5}cos2x\right)+5=\dfrac{5}{2}sin\left(2x-a\right)+5\) (với \(cosa=\dfrac{3}{5}\))
\(\Rightarrow-\dfrac{5}{2}+5\le y\le\dfrac{5}{2}+5\)
b.
\(\Leftrightarrow y.sinx-2y.cosx+4y=3sinx-cosx+1\)
\(\Leftrightarrow\left(y-3\right)sinx+\left(1-2y\right)cosx=1-4y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(y-3\right)^2+\left(1-2y\right)^2\ge\left(1-4y\right)^2\)
\(\Leftrightarrow11y^2+2y-9\le0\)
\(\Leftrightarrow-1\le y\le\dfrac{9}{11}\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 7 2021
c.
Do \(x^2+y^2=1\Rightarrow\) đặt \(\left\{{}\begin{matrix}x=sina\\y=cosa\end{matrix}\right.\)
\(\Rightarrow y=\dfrac{2\left(sin^2a+6sina.cosa\right)}{1+2sina.cosa+cos^2a}=\dfrac{1-cos2a+6sin2a}{1+sin2a+\dfrac{1+cos2a}{2}}=\dfrac{2-2cos2a+12sin2a}{3+2sin2a+cos2a}\)
\(\Leftrightarrow3y+2y.sin2a+y.cos2a=2-2cos2a+12sin2a\)
\(\Leftrightarrow\left(2y-12\right)sin2a+\left(y+2\right)cos2a=2-3y\)
Theo điều kiện có nghiệm của pt bậc nhất theo sin2a, cos2a:
\(\left(2y-12\right)^2+\left(y+2\right)^2\ge\left(2-3y\right)^2\)
\(\Leftrightarrow y^2+8y-36\le0\)
\(\Rightarrow-4-2\sqrt{13}\le y\le-4+2\sqrt{13}\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Hàm số \(y = \sin 2x + \tan 2x\) có nghĩa khi \(tan 2x\) có nghĩa
\(\cos 2x \ne 0\;\; \Leftrightarrow 2x \ne \frac{\pi }{2}\;\;\;\; \Leftrightarrow x \ne \frac{\pi }{4} + \frac{{k\pi }}{2}\) \
Vây tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - 2x} \right) + \tan \left( { - 2x} \right) = - \sin 2x - \tan 2x = - \left( {\sin 2x + \tan 2x} \right) = - f\left( x \right),\;\forall x \in D\).
Vậy \(y = \sin 2x + \tan 2x\) là hàm số lẻ
b) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cos \left( { - x} \right) + {\sin ^2}\left( { - x} \right) = \cos x + {\sin ^2}x = f\left( x \right),\;\forall x \in D\)
Vậy \(y = \cos x + {\sin ^2}x\) là hàm số chẵn
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
c) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right)\cos \left( { - 2x} \right) = - \sin x.\cos 2x = - f\left( x \right),\;\forall x \in D\)
Vậy \(y = \sin x\cos \;2x\) là hàm số lẻ
d) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) + \cos \left( { - x} \right) = - \sin x + \cos x \ne f\left( x \right),\;\forall x \in D\)
Vậy \(y = \sin x + \cos x\) không là hàm số chẵn cũng không là hàm số lẻ
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có: \(y = \cos x\)
\(y\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = y\)
Suy ra hàm số \(y = \cos x\) là hàm số chẵn
Vậy ta chọn đáp án C
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2020
\(cosa=cos\left(2\pi-a\right)\)
Mà \(t=2\pi-\left(x+y+z\right)\) nên...
tư mã chiêu
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Biểu thức \(\frac{{1 - \cos x}}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)
b) Biểu thức \(\sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} \) có nghĩa khi \(\left\{ {\begin{array}{*{20}{c}}{\frac{{1 + \cos x}}{{2 - \cos x}} \ge 0}\\{2 - \cos x \ne 0}\end{array}} \right.\)
Vì \( - 1 \le \cos x \le 1 ,\forall x \in \mathbb{R}\)
Vậy tập xác định của hàm số là \(D = \mathbb{R}\)
8 tháng 4 2022
ơ bạn :\(\dfrac{cos\left(x+y\right)+cosx}{cos\left(x+y\right)-cosx}=\dfrac{2cos\left(\dfrac{2x+y}{2}\right).cos\left(\dfrac{y}{2}\right)}{-2sin\left(\dfrac{2x+y}{2}\right).sin\left(\dfrac{y}{2}\right)}=-2.cot\left(\dfrac{2x+y}{2}\right).cot\left(\dfrac{y}{2}\right)\) L không thể bẳng 0 được
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
Đề lỗi font. Bạn cần chỉnh sửa lại bằng công thức toán để được hỗ trợ tốt hơn.