Cho tam giác ABC cân tại A ( AB=AC) AC=10cm;BC=12cm.Gọi H là trung điểm của BC. Vẽ HE vuông góc AB tại E và HF vuông góc AC tại F.
a) Tính AH
b) Chứng minh BE=CF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 7 2017
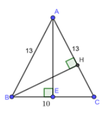
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
=> E là trung điểm BC => EB = EC = 5
Xét ABE vuông tại E có:
Mặt khác:
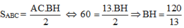
Xét ABH vuông tại H có:
Đáp án cần chọn là: A
T
1
31 tháng 8 2017
kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)
CM
23 tháng 2 2018
Tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao.
Có BM = BC/2 = 6cm
Áp dụng định lí Pytago trong tam giác vuông ABM có:
AM2 = AB2 - BM2 = 102 - 62 = 64 ⇒ AM = 8m. Chọn C
16 tháng 2 2022
https://hoc24.vn/cau-hoi/.4762222558882
-Bạn chỉ cần thay đổi một chút thôi.
CM
28 tháng 1 2018
Vì BD là đường phân giác của A B C ^ nên: A D D C = A B B C
Suy ra: A D D C + A D = A B B C + A B (theo tính chất dãy tỉ số bằng nhau)
⇒ A D A C = A B B C + A B
Mà tam giác ABC cân tại A nên AC = AB = 15cm
Đáp án: C
11 tháng 1 2022
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
Câu a :
Ta có :
AB=10cm
BC=12cm⇒HB=HC=6cm
AH=?
Theo định lý py - ta - go ta có :
AH2=AB2−HB2
AH2=102−62
AH2=64
⇒AH=8cm
Câu b :
Xét Δvuông HEBvà HFCcó :
HB=HC(gt)
HEBˆ=HFCˆ(900)
⇒ΔHEB=ΔHFC(ch−gv)
⇒BE=CF ( 2 cạnh tương ứng )
A B C H E F
a, Vì H là trung điểm của BC nên BH = CH =\(\frac{BC}{2}=\frac{12}{2}\) = 6cm
mà AB = AC nên A thuộc đường trung trực của BC
=> AH là đường trung trực của BC
=> AH vuông góc với BC
Áp dụng định lý Pytago vào tam giác vuông AHB có :
\(AH^2=AB^2-BH^2\)
\(\Rightarrow AH^2=10^2-6^2\)
\(\Rightarrow AH^2=64\)
\(\Rightarrow AH=8cm\)
Vậy AH = 8cm .
b, Xét hai tam giác vuông BHE và tam giác CHF có :
góc BEH = góc CFH = 90độ
BH = CH
góc B = góc C ( vì tam giác ABC cân tại A )
Do đó : tam giác BHE = tam giác CHF ( cạnh huyền - góc nhọn )
=> BE = CF
-> đpcm
Học tốt