Cho hình bình hành ABCD. Đường tròn (O;R) đi qua A và B, đường tròn (I;R) đi qua B và C.(O) và (I) cắt nhau tại điểm thứ 2 là M. CMR: bán kính đường tròn ngoại tiếp tam giác ADM bằng R.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 4 2020
Bài này bạn chia làm 2 trường hợp Q thuộc đoạn AD và Q nằm ngoài AD
- Trường hợp 1
Từ gt => OA=5, OQ=4, và OM=ON=OP=3
Áp dụng định lý Pytago cho các tam giác QAO và tam giác MAO vuông ứng ứng lần lượt tại Q và M ta có:
AQ2=AO2-OQ2=52-42=32 => AQ+3
AM2=AO2-OM2=52-32=42 => AM=4
=> AM=QO và AQ=MO => AMOQ là hình bình hành
Mà \(\widehat{AMO}=90^o\) => AMOQ là hình chữ nhật
=> \(\widehat{QAM}=90^o\)
Từ đó ta có ABCD là hình chữ nhật
Đặt CP=CN=x
Áp dụng định lý Pytago cho tam giác ABC vuông tại B, với BM=ON=3
AP=AM=4; AB=AM+BM=7
ta có: CA2=AB2+BC2 <=> (x+4)2=72+(x+3)2
=> x=21 và BC=24
Vậy diện tích hình bình hành ABCD là 7.24=168 (đv diện tích)
9 tháng 4 2020
- Trường hợp 2: Q nằm ngoài đoạn AD
Cmtt trường hợp 1 ta tính được
\(\widehat{ACB}=90^o;AC=7;BC=24\)
Từ đó ta tính được
SABCD=168 (đv diện tích)
28 tháng 6 2023
a: góc DMC=góc DBC=90 độ
=>DMBC nội tiếp đường tròn đường kính dC
I là trung điểm của DC
b: góc ANB=1/2*180=90 độ
=>ΔANB vuông tại N
=>góc NAB+góc NBA=90 độ và DM//BN
Gọi K là giao của AC và BD
=>K là trung điểm chung của AC và BD
Xét ΔKDM vuông tại M và ΔKBN vuông tại N có
KD=KB
góc DKM=góc BKN
=>ΔKDM=ΔKBN
=>DM=BN
mà DM//BN
nên DMBN là hình bình hành
=>góc MBD=góc BDN=góc MCD
Xét ΔDAC và ΔNBD có
góc DCA=góc NDB
góc DAC=góc NBD
=>ΔDAC đồng dạng với ΔNBD
=>DC/DN=AC/BD
=>DC*DB=DN*CA
HQ
Hà Quang Minh
Giáo viên
8 tháng 10 2023
a) O là trung điểm của AB, Khi đó AB là đường kính của đường tròn.
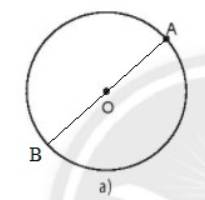
b) Độ dài IM = IM'.
CM
25 tháng 11 2017
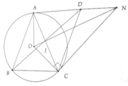
a, Tam giác ABC cân tại A nội tiếp (O)
=> OA ⊥ BC
=> OA ⊥ AD (vì AD//BC)
=> AD là tiếp tuyến của (O)
b, Chứng minh được ON là tia phân giác của A O D ^ mà ∆OAC cân tại O nên ON cũng là đường trung tuyến => ON cắt AC tại trung điểm I của AC => ON,AC,BD cùng đi qua trung điểm I của AC