cho góc nhọn xOy. gọi M là 1 điểm thuộc tia phân giác của góc xOy. kẻ MA VUÔNG GÓC VỚI Ox; KẺ MB VUÔNG GÓC VỚI Oy
a, chứng minh MA = MB và tam giác OAB là tam giác cân
b, đường BM cắt Ox tại D , đường thẳng AM cắt Oy tại E . CHỨNG MINH MD=ME
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 2 2016
Câu b:Xét tam giác BME và tam giác AMD:
góc B = góc A
MB=MA
góc BME = góc AMD
suy ra: tam giác BME = tam giác AMD
suy ra: MD=ME
Câu a:Xét tam giác OBM và tam giác OAM ta có
OA chung
Góc BOM = góc AOM
góc B= góc A
suy ra: tam giác OBM = tam giác OAM
suy ra: MA=MB
và suy ra: OA=OB ; tam giác OAB là tam giác cân tại O vì OA=OB
12 tháng 6 2020
ngu\(\hept{\begin{cases}3\\3\end{cases}\hept{\begin{cases}5\\5\\5\end{cases}}5555555b5b5b55b}\)
11 tháng 7 2023
a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
=>MA=MB và OA=OB
b: M đối xứng D qua Ox
=>OM=OD
M đối xứng E qua Oy
=>OE=OM
=>OD=OE
NV
9 tháng 5 2022
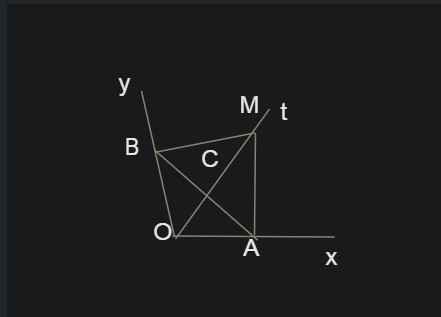
a) Xét tam giác vuông AMO và tam giác vuông BMO :
góc MOA = góc MOB (gt)
OM là cạnh chung
=>tam giác vuông AMO = tam giác vuông BMO (cạnh huyền + góc nhọn)
=> OA=OB ( 2 cạnh tương ứng)
b) theo a) ta có : tam giác AMO = tam giác BMO
=>góc AMO = góc BMO
=> MO là tia phân giác của góc AMB
c) gọi C là giao điểm của OM và AB
Xét tam giác OAC và tam giác OBC có:
góc AOC = góc BOC (gt)
OC là cạnh chung
OA = OB (theo a)
=>tam giác OAC = tam giác OBC
=> góc ACO = góc BCO
mà hai góc này kề bù
=> góc ACO = góc BCO = 90 độ
=> OM vuông góc với AB
23 tháng 6 2020
tự kẻ hình nha
a) vì M thuộc tia phân giác của xOy=> M cách đều Ox,Oy=> MA=MB
xét tam giác OBM và tam giác OAM có
OBM=OAM(=90 độ)
OM chung
BOM=AOM( gt)
=> tam giác OBM= tam giác OAM(ch-gnh)
=> OA=OB( hai cạnh tương ứng)
=> tam giác ABO cân O
b) vì M thuộc tia phân giác của góc xOy=>ME=MD
c) vì BD,AE,OM cùng giao nhau tại M
mà BD,AE là đường cao => OM là đường cao ( 3 đường cao cùng đi qua một điểm)
=> OM vuông góc với DE
22 tháng 2 2022
a: Xét ΔOMA vuông tại A và ΔOMB vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOMA=ΔOMB
Suy ra: MA=MB và OA=OB
hay ΔOBA cân tại O
b: Xét ΔOAE vuông tại A và ΔOBD vuông tại B có
OA=OB
\(\widehat{AOE}\) chung
Do đó: ΔOAE=ΔOBD
Suy ra: OD=OE
Xét ΔMAD vuông tại A và ΔMBE vuông tại B có
AD=BE
\(\widehat{MDA}=\widehat{MEB}\)
Do đó: ΔMAD=ΔMBE
Suy ra: MD=ME
c: Ta có: ΔODE cân tại O
mà OM là phân giác
nên OM vuông góc với DE
21 tháng 3 2022
a: Xét ΔOAC vuông tại A và ΔOBC vuông tại B có
OC chung
\(\widehat{AOC}=\widehat{BOC}\)
Do đó: ΔOAC=ΔOBC
Suy ra: OA=OB và CA=CB
=>ΔOAB cân tại O
b: Ta có: OA=OB
CA=CB
DO đó: OC là đường trung trực của AB
hay OC\(\perp\)AB
c: Xét ΔCAD vuông tại A và ΔCBE vuông tại B có
CA=CB
\(\widehat{ACD}=\widehat{BCE}\)
Do đó: ΔCAD=ΔCBE
SUy ra: CD=CE
Câu b:Xét tam giác BME và tam giác AMD:
góc B = góc A
MB=MA
góc BME = góc AMD
suy ra: tam giác BME = tam giác AMD
suy ra: MD=ME