Có bao nhiêu giá trị nguyên dươg của tham số m để hàm số
\(y=\sqrt{x+m}-\frac{1}{2x-m+1}\)
xác định trên \(\left(1;2\right)\cup\left[4;+\infty\right]\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left(m+1\right)x\ge-2m-3\)
- Với \(m=-1\) thỏa mãn
- Với \(m>-1\Rightarrow x\ge\dfrac{-2m-3}{m+1}\)
\(\Rightarrow\dfrac{-2m-3}{m+1}\le-3\) \(\Leftrightarrow\dfrac{2m+3}{m+1}-3\ge0\Leftrightarrow\dfrac{-m}{m+1}\ge0\)
\(\Rightarrow-1< m\le0\Rightarrow m=0\)
- Với \(m< -1\Rightarrow x\le\dfrac{-2m-3}{m+1}\Rightarrow\dfrac{-2m-3}{m+1}\ge-1\)
\(\Rightarrow\dfrac{2m+3}{m+1}-1\le0\Leftrightarrow\dfrac{m+2}{m+1}\le0\)
\(\Rightarrow-2\le m< -1\Rightarrow m=-2\)
Vậy \(m=\left\{-2;-1;0\right\}\)

Hàm số y = ln x 2 - 2 x - m + 1 xác định trên R
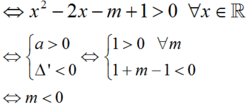
Mà
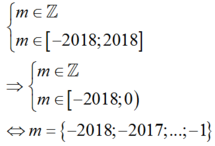
Vậy có 2018 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn A.

Chọn C
Hàm số y = ln ( x 2 - 2 x - m + 1 ) có tập xác định là ℝ khi và chỉ khi:
![]()
![]()

1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)
Lời giải:
Để $y$ xác định trên trên $(1;2)\cup [4;+\infty)$ thì:
\(\left\{\begin{matrix} x+m\geq 0\\ 2x-m+1\neq 0\end{matrix}\right., \forall x\in (1;2)\cup [4;+\infty)\)
\(\Leftrightarrow \left\{\begin{matrix} -m\leq x\\ m\neq 2x+1\end{matrix}\right., \forall x\in (1;2)\cup [4;+\infty)\)
\(\Leftrightarrow \left\{\begin{matrix} -m\leq 1\\ m\neq (3;5)\cup [9;+\infty)\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\geq -1\\ m\in (-\infty;3]\cup [5;9)\end{matrix}\right.\)
Vì $m$ nguyên dương nên $m\in\left\{1;2;3;5;6;7;8\right\}$
Tức là có 7 giá trị $m$ thỏa mãn.