Giải phương trình sau:
(24x2+19x+2). √(5x2 +4x+2)= (7x2+3x+5). √(8x+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 6 2018
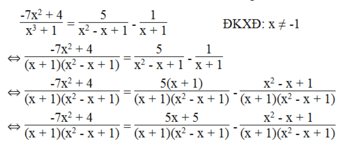
⇔ -7 x 2 + 4 = 5x + 5 – x 2 + x – 1
⇔ -7 x 2 + x 2 – 5x – x = 5 – 1 – 4
⇔ -6 x 2 – 6x = 0
⇔ - x 2 – x = 0
⇔ x(x + 1) = 0
⇔ x = 0 hoặc x + 1 = 0
⇔ x = 0 hoặc x = -1 (loại)
Vậy phương trình có nghiệm x = 0.
29 tháng 8 2021
a: Ta có: \(3x+5\le4x-9\)
\(\Leftrightarrow-x\le-14\)
\(\Leftrightarrow x\ge14\)
b: Ta có: \(6-2x< 6-x\)
\(\Leftrightarrow-x< 0\)
hay x>0
c: Ta có: \(7\left(x-1\right)+5>-3x\)
\(\Leftrightarrow7x-7+5+3x>0\)
\(\Leftrightarrow10x>2\)
hay \(x>\dfrac{1}{5}\)
AH
Akai Haruma
Giáo viên
10 tháng 12 2021
1/ ĐKXĐ: $4x^2-4x-11\geq 0$
PT $\Leftrightarrow \sqrt{4x^2-4x-11}=2(4x^2-4x-11)-6$
$\Leftrightarrow a=2a^2-6$ (đặt $\sqrt{4x^2-4x-11}=a, a\geq 0$)
$\Leftrightarrow 2a^2-a-6=0$
$\Leftrightarrow (a-2)(2a+3)=0$
Vì $a\geq 0$ nên $a=2$
$\Leftrightarrow \sqrt{4x^2-4x-11}=2$
$\Leftrightarrow 4x^2-4x-11=4$
$\Leftrightarrow 4x^2-4x-15=0$
$\Leftrightarrow (2x-5)(2x+3)=0$
$\Rightarrow x=\frac{5}{2}$ hoặc $x=\frac{-3}{2}$ (tm)
AH
Akai Haruma
Giáo viên
10 tháng 12 2021
2/ ĐKXĐ: $x\in\mathbb{R}$
PT $\Leftrightarrow \sqrt{3x^2+9x+8}=\frac{1}{3}(3x^2+9x+8)-\frac{14}{3}$
$\Leftrightarrow a=\frac{1}{3}a^2-\frac{14}{3}$ (đặt $\sqrt{3x^2+9x+8}=a, a\geq 0$)
$\Leftrightarrow a^2-3a-14=0$
$\Rightarrow a=\frac{3+\sqrt{65}}{2}$ (do $a\geq 0$)
$\Leftrightarrow 3x^2+9x+8=\frac{37+3\sqrt{65}}{2}$
$\Rightarrow x=\frac{1}{2}(-3\pm \sqrt{23+2\sqrt{65}})$
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 2 2021
1.
ĐKXĐ: \(x\ge-\dfrac{1}{3}\)
\(\Leftrightarrow3x^2-3x+\left(x+1-\sqrt{3x+1}\right)+\left(x+2-\sqrt{5x+4}\right)=0\)
\(\Leftrightarrow3\left(x^2-x\right)+\dfrac{x^2-x}{x+1+\sqrt{3x+1}}+\dfrac{x^2-x}{x+2+\sqrt{5x+4}}=0\)
\(\Leftrightarrow\left(x^2-x\right)\left(3+\dfrac{1}{x+1+\sqrt{3x+1}}+\dfrac{1}{x+2+\sqrt{5x+4}}\right)=0\)
\(\Leftrightarrow x^2-x=0\)
\(\Leftrightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 2 2021
2.
Đặt \(\left\{{}\begin{matrix}2x=a\\\sqrt[3]{2-8x^3}=b\end{matrix}\right.\)
Ta được hệ:
\(\left\{{}\begin{matrix}\left(2a-1\right)b=a\\a^3+b^3=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=2ab\\\left(a+b\right)^3-3ab\left(a+b\right)=2\end{matrix}\right.\)
\(\Rightarrow8\left(ab\right)^3-6\left(ab\right)^2=2\)
\(\Leftrightarrow\left(ab-1\right)\left[4\left(ab\right)^2+ab+1\right]=0\)
\(\Leftrightarrow ab=1\Rightarrow a+b=2\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=2\\ab=1\end{matrix}\right.\) \(\Leftrightarrow a=b=1\)
\(\Rightarrow2x=1\Rightarrow x=\dfrac{1}{2}\)
PA
2
HP
3 tháng 10 2021
a. 3x2 - 4y2 = 18
<=> \(\left\{{}\begin{matrix}3x^2=18+4y^2\\4y^2=-\left(3x^2-18\right)\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{\dfrac{18+4y^2}{3}}\\y=\sqrt{\dfrac{-3x^2+18}{4}}\end{matrix}\right.\)
b, c, d tương tự nhé
HP
3 tháng 10 2021
b. 19x2 + 28y2 = 2001
<=> \(\left\{{}\begin{matrix}19x^2=2001-28y^2\\28y^2=2001-19x^2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{\dfrac{2001-28y^2}{19}}\\y=\sqrt{\dfrac{2001-19x^2}{28}}\end{matrix}\right.\)
c. x2 = 2y2 - 8y + 3
<=> \(\left\{{}\begin{matrix}x=\sqrt{2y^2-8y+3}\\8y=2y^2+3-x^2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{2y^2-8y+3}\\y=\dfrac{2y^2+3-x^2}{8}\end{matrix}\right.\)
d. x2 + y2 - 4x + 4y = 1
<=> \(\left\{{}\begin{matrix}x^2=1-y^2+4x-4y\\y^2=1-x^2+4x-4y\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{1-y^2+4x-4y}\\y=\sqrt{1-x^2+4x-4y}\end{matrix}\right.\)