Cho \(cot\varphi=a\).Tính theo a giá trị của \(sin\left(2\varphi-\frac{\pi}{4}\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 9 2020
\(cotb=a\Rightarrow\frac{cosb}{sinb}=a\Rightarrow cosb=a.sinb\)
\(sin\left(2b-\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\left(sin2b-cos2b\right)\)
\(=\sqrt{2}sinb.cosb-\frac{\sqrt{2}}{2}\left(1-2sin^2b\right)=a\sqrt{2}sin^2b+\sqrt{2}sin^2b-\frac{\sqrt{2}}{2}\)
\(=\left(a\sqrt{2}+\sqrt{2}\right)sin^2b-\frac{\sqrt{2}}{2}=\left(a\sqrt{2}+\sqrt{2}\right).\frac{1}{1+cot^2b}-\frac{\sqrt{2}}{2}\)
\(=\frac{a\sqrt{2}+\sqrt{2}}{1+a^2}-\frac{\sqrt{2}}{2}\)
AH
Akai Haruma
Giáo viên
12 tháng 7 2017
Câu a)
Đặt \(y=\sqrt{t}\Rightarrow I_1=\int ^{1}_{0}(y-1)^2\sqrt{y}dy=\int ^{1}_{0}(t^2-1)^2td(t^2)\)
\(\Leftrightarrow I_1=2\int^{1}_{0}(t^2-1)^2t^2dt=2\int ^{1}_{0}(t^6-2t^4+t^2)dt\)
\(=2\left.\begin{matrix} 1\\ 0\end{matrix}\right|\left ( \frac{t^7}{7}-\frac{2t^5}{5}+\frac{t^3}{3} \right )=\frac{16}{105}\)
b) Đặt \(u=\sqrt[3]{z-1}\Rightarrow z=u^3+1\Rightarrow I_2=\int ^{1}_{0}[(u^3+1)^2+1]u^2d(u^3+1)\)
\(\Leftrightarrow I_2=3\int ^{1}_{0}[(u^3+1)^2+1]u^4du=3\int ^{1}_{0}(u^{10}+2u^7+2u^4)du\)
\(=3\left.\begin{matrix} 1\\ 0\end{matrix}\right|\left ( \frac{x^{11}}{11}+\frac{x^8}{4}+\frac{2x^5}{5} \right )=\frac{489}{220}\)
AH
Akai Haruma
Giáo viên
12 tháng 7 2017
c) Ta có:
\(I_3=\int ^{e}_{1}\frac{\sqrt{4+5\ln x}}{x}dx=\int ^{e}_{1}\sqrt{4+5\ln x}d(\ln x)\)
Đặt \(\sqrt{4+5\ln x}=t\Rightarrow I_3=\int ^{3}_{2}td\left (\frac{t^2-4}{5}\right)=\frac{2}{5}\int ^{3}_{2}t^2dt=\frac{38}{15}\)
d)
Xét \(\int ^{\frac{\pi}{2}}_{0}\cos ^5xdx=\int ^{\frac{\pi}{2}}_{0}\cos ^4xd(\sin x)=\int ^{\frac{\pi}{2}}_{0}(1-\sin ^2x)^2d(\sin x)\)
\(=\int ^{1}_{0}(1-t^2)^2dt\)
Xét \(\int ^{\frac{\pi}{2}}_{0}\sin ^5xdx=-\int ^{\frac{\pi}{2}}_{0}\sin ^4xd(\cos x)=-\int ^{\frac{\pi}{2}}_{0}(1-\cos ^2x)^2d(\cos x)=\int ^{1}_{0}(1-t^2)^2dt\)
Do đó \(\int ^{\frac{\pi}{2}}_{0}(\cos ^5x-\sin ^5x)dx=0\)
e)
Có \(\int \cos ^3x\cos 3xdx=\int \cos 3x\left ( \frac{3\cos x+\cos 3x}{4} \right )dx=\frac{1}{4}\int \cos ^23xdx+\frac{3}{4}\int \cos x\cos 3xdx\)
\(=\frac{1}{8}\int (1+\cos 6x)dx+\frac{3}{8}\int (\cos 4x+\cos 2x)dx\)
\(=\frac{1}{8}\int (1+\cos 6x)dx+\frac{3}{8}\int (\cos 4x+\cos 2x)dx=\frac{x}{8}+\frac{\sin 6x}{48}+\frac{3\sin 4x}{32}+\frac{3\sin 2x}{16}\)
Suy ra \(\int ^{\pi}_{0}\cos ^3x\cos 3xdx=\frac{\pi}{8}\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cot \left( { - x} \right) = - \cot x = - f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \cot x\) là hàm số lẻ.
b)
\(x\) | \(\frac{\pi }{6}\) | \(\frac{\pi }{4}\) | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\frac{{3\pi }}{4}\) | \(\frac{{5\pi }}{6}\) |
\(\cot x\) | \(\sqrt 3 \) | \(1\) | \(\frac{{\sqrt 3 }}{3}\) | \(0\) | \( - \frac{{\sqrt 3 }}{3}\) | \( - 1\) | \( - \sqrt 3 \) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \cot x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\).
SS
29 tháng 7 2016
Mạch thuần C nên i sớm pha hơn u góc \(\frac{\pi}{2}\)
\(\varphi_u-\varphi_i=-\frac{\pi}{2}\Rightarrow\frac{\pi}{4}-\varphi=-\frac{\pi}{2}\Rightarrow\varphi=\frac{3\pi}{4}\)
19 tháng 11 2015
Trong mạch dao động thì i sớm pha hơn q là \(\frac{\pi}{2}.\)
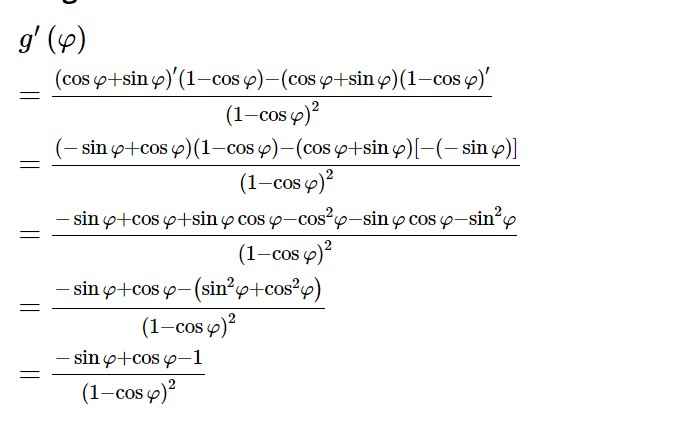
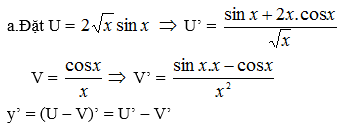
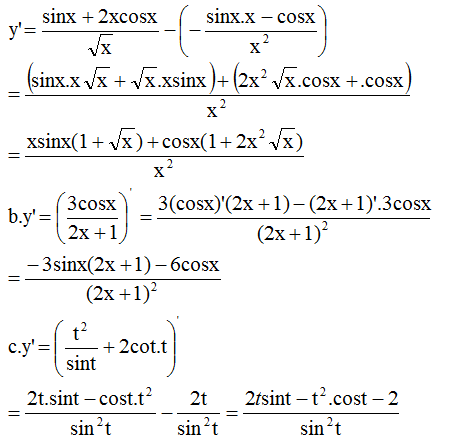
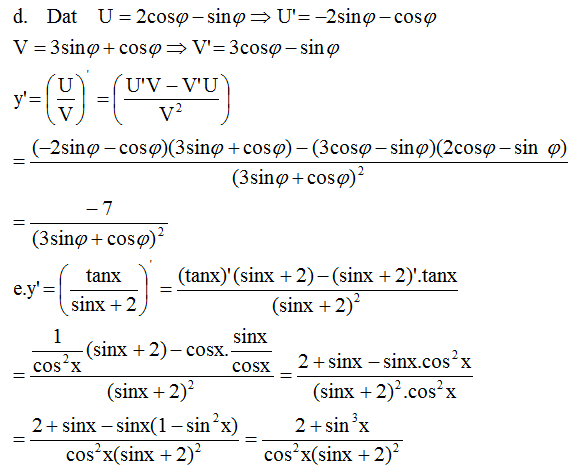
Có: \(sin^2\phi=\frac{1}{1+cot^2\phi}=\frac{1}{a^2+1}\), Từ đây ta được các đẳng thức:
\(sin2\phi=2sin\phi cos\phi=2cot\phi sin^2\phi=\frac{2a}{a^2+1}\)
\(cos2\phi=1-2sin^2\phi=1-\frac{2}{a^2+1}=\frac{a^2-1}{a^2+1}\)
Xét: \(sin\left(2\phi-\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\left(sin2\phi-cos2\phi\right)=\frac{\sqrt{2}}{2}\left(\frac{2a}{a^2+1}-\frac{a^2-1}{a^2+1}\right)=-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}\left(a+1\right)}{a^2+1}\)