Cho hàm số \(y=\frac{2mx-3}{x-1}\) và đường thẳng d: y = x + 1. Với giá trị nào của m thì d cắt đồ thị hàm số tại hai điểm phân biệt A, B đối xứng nhau qua đường thẳng d1: y = - x + 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Để hàm số y=(m-1)x+3 đồng biến trên R thì m-1>0
=>m>1
Để hàm số y=(m-1)x+3 nghịch biến trên R thì m-1<0
=>m<1
b: Thay m=3 vào (d), ta được:
\(y=\left(3-1\right)x+3=2x+3\)
Vẽ đồ thị:
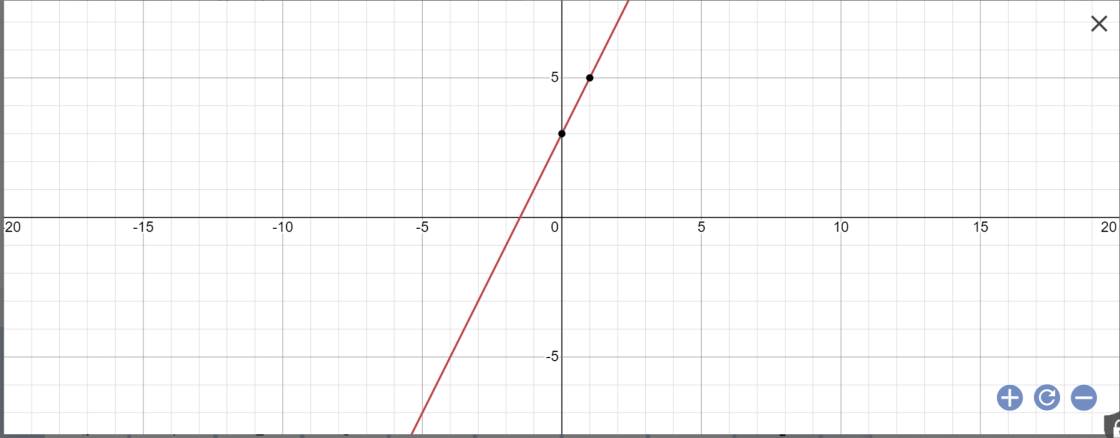
c: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-1=2\\3\ne-1\left(đúng\right)\end{matrix}\right.\)
=>m-1=2
=>m=3
d: Thay x=-2 và y=0 vào (d1), ta được:
\(-2\left(m-1\right)+3=0\)
=>-2(m-1)=-3
=>\(m-1=\dfrac{3}{2}\)
=>\(m=\dfrac{3}{2}+1=\dfrac{5}{2}\)

Đáp án B
2 x + 3 x + 2 = x + m ⇔ 2 x + 3 = x 2 + m x + 2 x + 2 m ⇔ f x = x 2 + m x + 2 m - 3 = 0 ( 1 )
Rõ ràng f - 2 ≠ 0 , ∀ m nên ta cần có ∆ > 0 ⇔ m 2 - 4 2 m - 3 > 0 ⇔ [ m > 6 m < 2 .

Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)

Đáp án A
+ Phương trình hoành độ giao điểm: ![]()
+ Điều kiện để d cắt tại hai điểm phân biệt là ![]() .
.
+ Trung điểm của MN là I.
+ Theo công thức đường trung tuyến 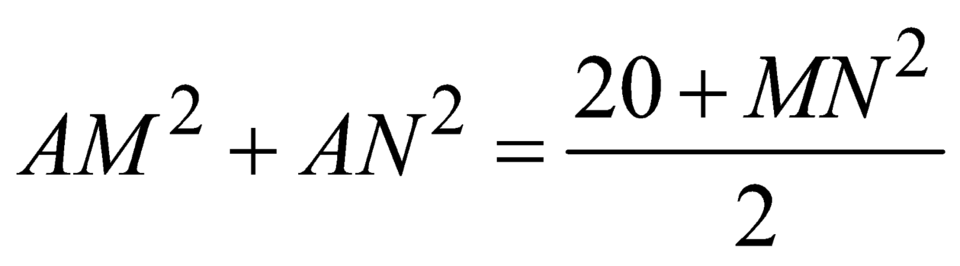 .
.
![]() nhỏ nhất khi
nhỏ nhất khi ![]() nhỏ nhất.
nhỏ nhất.
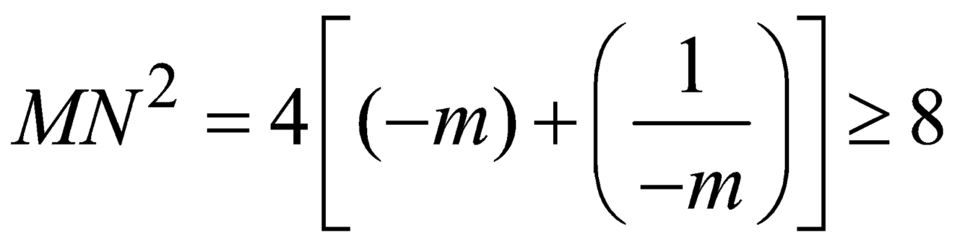 , dấu bằng xảy ra khi
, dấu bằng xảy ra khi ![]()

a: Để hai đường thẳng song song thì m-1=3-m
=>2m=4
hay m=2
\(\text{//}\Leftrightarrow m-1=3-m\Leftrightarrow m=2\\ \cap\Leftrightarrow m-1\ne3-m\Leftrightarrow m\ne2\)



Lời giải:
PT hoành độ giao điểm:
$\frac{2mx-3}{x-1}=x+1$
$\Leftrightarrow x^2-2mx+2=0(*)$
Để 2 ĐTHS cắt nhau tại 2 điểm $A,B$ thì PT $(*)$ có 2 nghiệm phân biệt $x_A,x_B$
$\Leftrightarrow \Delta'=m^2-2>0$
Áp dụng định lý Viet: $x_A+x_B=2m$
$A,B$ đối xứng với nhau qua đường thẳng $d_1$ thì $d_1$ đi qua trung điểm của $AB$
$\Leftrightarrow (\frac{x_A+x_B}{2}, \frac{y_A+y_B}{2})\in d_1$
$\Leftrightarrow \frac{y_A+y_B}{2}=-\frac{x_A+x_B}{2}+7$
$\Leftrightarrow \frac{x_A+1+x_B+1}{2}=-\frac{x_A+x_B}{2}+7$
$\Leftrightarrow x_A+x_B=6$
$\Leftrightarrow 2m=6\Leftrightarrow m=3$ (thỏa mãn)