Cho tam giác ABC có A<120\(^o\)
Tìm điểm M \(\in\)tam giác ABC sao cho tổng MA+MB+MC là nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2016
A B C M D E N P
Ta dựng các tam giác đều AMP , AMN , ACE , ABD , suy ra N,P,E,D cố định.
Dễ dàng chứng minh được \(\Delta APE=\Delta AMC\left(c.g.c\right)\)
\(\Rightarrow MC=PE\), \(AM=MP\)
Suy ra : \(AM+MC+BM=BM+MP+PE\ge BE\)(hằng số)
Tương tự , ta cũng chứng minh được \(AM=MN\), \(BM=DN\)
\(\Rightarrow AM+MC+MB=CM+MN+DN\ge CD\)(hằng số)
Suy ra MA + MB + MC đạt giá trị nhỏ nhất khi M là giao điểm của BE và CD.
Cần chú ý : Vì điều kiện các góc của tam giác nhỏ hơn 180 độ :
\(\widehat{BAC}+\widehat{CAE}< 120^o+60^o=180\)
\(\widehat{BAC}+\widehat{BAD}< 120^o+60^o=180^o\)
nên BE cắt AC tại một điểm nằm giữa A và C , CD cắt AB tại một điểm nằm giữa A và B. Do đó tồn tại giao điểm M của CD và BE.
CM
27 tháng 2 2019
Trong ∆ ABC ta lấy điểm M. Nối MA, MB, MC.
Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.
Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.
Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Khi đó, CA = CP
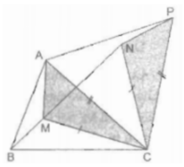
Xét ∆ AMC và ∆ PNC:
CM = CN (vì ΔMCN đều)
CA = CP (vì ΔAPC đều)
Suy ra: ∆ AMC = ∆ PNC (c.g.c)
⇒ PN = AM
MA + MB + MC = NP + MB + MN
Ta có ∆ ABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.
16 tháng 12 2023
Chị ơi giúp e cái này tìm 3 giá trị của x sao cho 0,6<x<0,61
MH
17 tháng 12 2023
Gọi I là tâm đường tròn nội tiếp tam giác ABC
\(\Rightarrow a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=0\)
Ta có:
\(A=\left|a\overrightarrow{MA}+b\overrightarrow{MB}+c\overrightarrow{MC}\right|=\left|\left(a+b+c\right)\overrightarrow{MI}+a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}\right|\)
\(=\left|\left(a+b+c\right)\overrightarrow{MI}\right|=\left(a+b+c\right).MI\)
\(Amin\Leftrightarrow MImin\)
\(\Leftrightarrow\) M trùng I
Bài giải
Ta dựng các tam giác đều AMP , AMN , ACE , ABD , suy ra N,P,E,D cố định.
Dễ dàng chứng minh được ΔAPE=ΔAMC(c.g.c)
⇒ MC = PE, AM = MP
Suy ra : AM + MC + BM = BM + MP + PE ≥ BE ( hằng số )
Tương tự , ta cũng chứng minh được AM = MN, BM = DN
⇒ AM + MC + MB = CM + MN + DN ≥ CD ( hằng số )
Suy ra MA + MB + MC đạt giá trị nhỏ nhất khi M là giao điểm của BE và CD.
Cần chú ý : Vì điều kiện các góc của tam giác nhỏ hơn 180 độ :
\(\widehat{BAC}+\widehat{CAE}\) < 120o + 60o = 180o
\(\widehat{BAC}+\widehat{BAD}\) < 120o + 60o = 180o
nên BE cắt AC tại một điểm nằm giữa A và C , CD cắt AB tại một điểm nằm giữa A và B. Do đó tồn tại giao điểm M của CD và BE.