Giải bất phương trình: |2x - 7| < x2 + 2x + 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 1 2021
TH1: \(\left\{{}\begin{matrix}2x-7\ge0\\2x-7< x^2+2x+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{7}{2}\\x^2>-9\end{matrix}\right.\) \(\Rightarrow x\ge\dfrac{7}{2}\)
TH2: \(\left\{{}\begin{matrix}2x-7< 0\\7-2x< x^2+2x+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{7}{2}\\x^2+4x-5>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{7}{2}\\\left[{}\begin{matrix}x>1\\x< -5\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}1< x< \dfrac{7}{2}\\x< -5\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x>1\\x< -5\end{matrix}\right.\)
B
Bài 1: Giải các bất phương trình sau
a) x+1/x+3 > 1
b) 2x-1/x-3 ≤ 2
c) x2+2x+2/x2+3 ≥ 1
d) 2x+1/x2+2 ≥ 1
2
13 tháng 4 2021
a, \(\dfrac{x+1}{x+3}>1\Leftrightarrow\dfrac{x+1}{x+3}-1>0\Leftrightarrow\dfrac{x+1-x-3}{x+3}>0\)
\(\Rightarrow x+3< 0\)do -2 < 0
\(\Rightarrow x< -3\)Vậy tập nghiệm BFT là S = { x | x < -3 }
b, \(\dfrac{2x-1}{x-3}\le2\Leftrightarrow\dfrac{2x-1}{x-3}-2\le0\Leftrightarrow\dfrac{2x-1-2x+6}{x-3}\le0\)
\(\Rightarrow x-3\le0\)do 5 > 0
\(\Rightarrow x\le3\)Vậy tập nghiệm BFT là S = { x | x \(\le\)3 }
c, \(\dfrac{x^2+2x+2}{x^2+3}\ge1\Leftrightarrow\dfrac{x^2+2x+2}{x^2+3}-1\ge0\)
\(\Leftrightarrow\dfrac{x^2+2x+2-x^2-3}{x^2+3}\ge0\Rightarrow2x-1\ge0\)do x^2 + 3 > 0
\(\Rightarrow x\ge\dfrac{1}{2}\)Vậy tập nghiệm BFT là S = { x | x \(\ge\)1/2 }
13 tháng 4 2021
mình ko chắc nên mình đăng sau :>
d, \(\dfrac{2x+1}{x^2+2}\ge1\Leftrightarrow\dfrac{2x+1}{x^2+2}-1\ge0\Leftrightarrow\dfrac{2x+1-x^2-2}{x^2+2}\ge0\)
\(\Rightarrow-x^2+2x-1\ge0\Rightarrow-\left(x-1\right)^2\ge0\)vô lí
6 tháng 4 2020
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
7 tháng 4 2020
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
HP
29 tháng 8 2021
1.
\(6+2x\ge3-x\)
\(\Leftrightarrow3x\ge-3\)
\(\Leftrightarrow x\ge-1\)
2.
\(2x+7>16-x\)
\(\Leftrightarrow3x>23\)
\(\Leftrightarrow x>\dfrac{23}{3}\)
3.
\(x-5< 3x+1\)
\(\Leftrightarrow2x>-6\)
\(\Leftrightarrow x>-3\)
KK
29 tháng 8 2021
Mik chưa học đến lớp 8 nên ko bt biểu diễn trên trục số nên chỉ tìm dc x thôi nha:
1. 6 + 2x \(\ge\) 3 - x
<=> 6 - 3 \(\ge\) -x - 2x
<=> 3 \(\ge\) -3x
<=> 3 : (-3) \(\ge\) -3x : (-3)
<=> -1 \(\le\) x
<=> x \(\ge\) -1
2. 2x + 7 > 16 - x
<=> 2x + x > 16 - 7
<=> 3x > 9
<=> 3x : 3 > 9 : 3
<=> x > 3
3. x - 5 < 3x + 1
<=> -5 - 1 < 3x - x
<=> -6 < 2x
<=> -6 : 2 < 2x : 2
<=> -3 < x
<=> x > (-3)
QT
2
14 tháng 6 2015
\(\sqrt{2x}\left(\frac{7}{2}+\frac{8}{2}\right)=\sqrt{2x}.7,5\)
Vì \(\sqrt{2x}\ge0\)
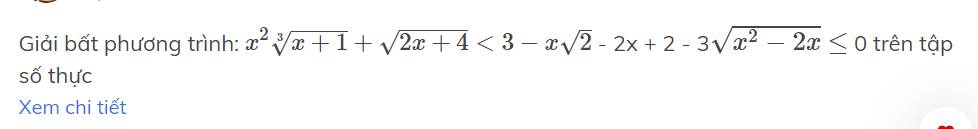
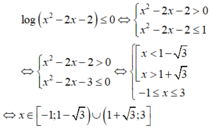
Do 2 vế đều ko âm, BPT tương đương:
\(\left(x^2+2x+2\right)^2>\left(2x-7\right)^2\)
\(\Leftrightarrow\left(x^2+2x+2\right)^2-\left(2x-7\right)^2>0\)
\(\Leftrightarrow\left(x^2+9\right)\left(x^2+4x-5\right)>0\)
\(\Leftrightarrow x^2+4x-5>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x< -5\\x>1\end{matrix}\right.\)