Tìm các số a và bc thỏa mãn a nhân bc = 259, trong đó a ko=1 và các chữ số a, b, c không nhất thiết phải khác nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 3 2017
Chọn B
Số phần tử của không gian mẫu 
Gọi biến cố A” Chọn được một số thỏa mãn 
”.
Vì mà nên trong các chữ số sẽ không có số 0.
TH1: Số được chọn có chữ số giống nhau có 9 số.
TH2: Số được chọn tạo bới hai chữ số khác nhau.
Số cách chọn ra 2 chữ số khác nhau từ 9 chữ số trên là: C 9 2 .
Mỗi bộ 2 chữ số được chọn tạo ra 2 số thỏa mãn yêu cầu.
Vậy có 2. C 9 2 số thỏa mãn.
TH3: Số được chọn tạo bởi ba chữ số khác nhau.
Số cách chọn ra 3 chữ số khác nhau từ 9 chữ số trên là: C 9 3 .
Mỗi bộ 3 chữ số được chọn chỉ tạo ra một số thỏa mãn yêu cầu.
Vậy có C 9 3 số thỏa mãn.
Vậy 
Xác suất của biến cố A là: .
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
26 tháng 12 2023
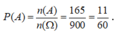
\(\dfrac{ab}{a+b}=\dfrac{bc}{b+c}=\dfrac{ca}{c+a}\)
\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{c}+\dfrac{1}{a}\)
\(\Rightarrow\dfrac{1}{a}=\dfrac{1}{b}=\dfrac{1}{c}=\dfrac{1+1+1}{a+b+c}=\dfrac{3}{a+b+c}=\dfrac{3}{1}=3\)
\(\Rightarrow a=b=c=\dfrac{1}{3}\)
\(\Rightarrow A=\dfrac{a^3\left(a^2+b^2+c^2\right)}{a^2+b^2+c^2}=a^3=\left(\dfrac{1}{3}\right)^3=\dfrac{1}{27}\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
\(Q=ac+bc-2022ab\le ac+bc=c\left(a+b\right)\le\dfrac{1}{4}\left(c+a+b\right)^2=\dfrac{1}{4}\)
\(Q_{max}=\dfrac{1}{4}\) khi \(\left\{{}\begin{matrix}a+b+c=1\\ab=0\\c=a+b\end{matrix}\right.\) \(\Leftrightarrow\left(a;b;c\right)=\left(0;\dfrac{1}{2};\dfrac{1}{2}\right);\left(\dfrac{1}{2};0;\dfrac{1}{2}\right)\)
\(Q=c\left(a+b\right)-2022ab\ge c\left(a+b\right)-\dfrac{1011}{2}\left(a+b\right)^2\)
\(Q\ge c\left(1-c\right)-\dfrac{1011}{2}\left(1-c\right)^2\)
\(Q\ge c\left(1-c\right)-\dfrac{1011}{2}c\left(c-2\right)-\dfrac{1011}{2}\)
\(Q\ge\dfrac{c\left(1011+1013\left(1-c\right)\right)}{2}-\dfrac{1011}{2}\ge-\dfrac{1011}{2}\)
\(Q_{min}=-\dfrac{1011}{2}\) khi \(\left(a;b;c\right)=\left(\dfrac{1}{2};\dfrac{1}{2};0\right)\)
16 tháng 7 2017
Từ giả thiết ta suy ra \(\hept{\begin{cases}abc-ab-bc-ac=0\\a+b+c-1=0\end{cases}}\)
\(\Rightarrow\left(abc-ab-bc-ac\right)+\left(a+b+c-1\right)=0\)
\(\Leftrightarrow\left(abc-ab\right)-\left(ac-a\right)-\left(bc-b\right)+\left(c-1\right)=0\)
\(\Leftrightarrow ab\left(c-1\right)-a\left(c-1\right)-b\left(c-1\right)+\left(c-1\right)=0\)
\(\Leftrightarrow\left(ab-a-b+1\right)\left(c-1\right)=0\)
\(\Rightarrow\left(a-1\right)\left(b-1\right)\left(c-1\right)=0\)
\(\Rightarrow\) Ít nhất một trong các số a;b;c phải bằng 1 (đpcm)
7 tháng 10 2015
gọi số đó là \(\overline{abcd}\) ở đó a,b,c,d thuộc {1,2,5,7}
a, để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng chữ số 5 hoặc 7.
vậy chữ số a có 2 cách chọn, chữ số b có 4 cách chọn
chữ số c có 4 cách chọn, d cũng có 4 cách chọn
suy ra có tất cả các chữ số ớn hơn 4000 là 2.4.4.4=128 số
b, để số đó lớn hơn 4000 thì chữ số a phải bắt đầu bằng 5 hoặc 7
mà các chữ số khác nhau
suy ra b có 3 cách chọn, c có 2 cách chọn và d có 1 cách chọn
số các chữ số cần tìm là: 2.3.2.1=12 số
Theo bài ra ta có
a là chữ số và a không bằng 1 nên \(1< a\le9\)
Xét các trường hợp
+) a = 2 thì \(\overline{bc}=259\div2=129,5\)( loại )
+) a = 3 thì \(\overline{bc}=259\div3=86,33\)( loại )
+) a = 4 thì \(\overline{bc}=259\div4=64,75\)( loại )
+) a = 5 thì \(\overline{bc}=259\div5=51,8\)( loại )
+) a = 6 thì \(\overline{bc}=259\div6\approx43,17\)( loại )
+) a = 7 thì \(\overline{bc}=259\div7=37\)( chọn )
+) a = 8 thì \(\overline{bc}=259\div8=32,375\)( loại )
+) a = 9 thì \(\overline{bc}=259\div9\approx27,78\)( loại )
Vậy a = 7, \(\overline{bc}=37\)