Giải phương trình
x2 + 7x + 12 = 0
giúp tuiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
6
Những câu hỏi liên quan
PT
1
CM
20 tháng 11 2017
a) x 2 – 7 x + 12 = 0
Có a = 1; b = -7; c = 12
⇒ Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 1 . 12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 thỏa mãn:
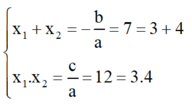
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là 3 và 4.
b) x2 + 7x + 12 = 0
Có a = 1; b = 7; c = 12
⇒ Δ = b2 – 4ac = 72 – 4.1.12 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn:
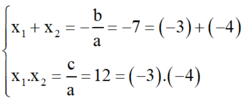
Vậy dễ dàng nhận thấy phương trình có hai nghiệm là -3 và -4.
PT
1
CM
21 tháng 4 2017
a) 3 x 2 – 7x + 2 = 0
Δ= 7 2 -4.3.2 = 49 - 24 = 25 > 0 ⇒ ∆ = 5
Phương trình có 2 nghiệm phân biệt:
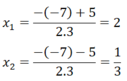
Vậy tập nghiệm của phương trình là S = {2; 1/3}
9 tháng 3 2023
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
NN
1
12 tháng 2 2023
\(\Leftrightarrow\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}+...+\dfrac{1}{\left(x+5\right)\left(x+6\right)}=\dfrac{1}{8}\)
=>\(\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}+...+\dfrac{1}{x+5}-\dfrac{1}{x+6}=\dfrac{1}{8}\)
=>1/x+2-1/x+6=1/8
=>\(\dfrac{x+6-x-2}{\left(x+2\right)\left(x+6\right)}=\dfrac{1}{8}\)
=>x^2+8x+12=32
=>x^2+8x-20=0
=>(x+10)(x-2)=0
=>x=-10 hoặc x=2
CM
1 tháng 7 2019
a) x 2 - 7x + 5 = 0
Δ = 7 2 - 4.1.5 = 49 - 20 = 29 > 0
⇒ Phương trình đã cho có 2 nghiệm phân biệt
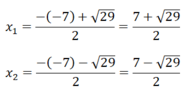
Vậy hệ phương trình đã cho có tập nghiệm
H
3 tháng 5 2023
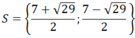
a, Thay \(m=1\) vào \(\left(1\right)\)
\(\Rightarrow x^2-7x+1=0\\ \Delta=\left(-7\right)^2-4.1.1=45\\ \Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{7+3\sqrt{5}}{2}\\x_2=\dfrac{7-3\sqrt{5}}{2}\end{matrix}\right.\)
b, \(\Delta=\left(-7\right)^2-4.m=49-4m\)
phương trình cs nghiệm \(49-4m\ge0\\ \Rightarrow m\le\dfrac{49}{4}\)
Áp dụng hệ thức vi ét
\(\left\{{}\begin{matrix}x_1+x_2=7\\x_1x_2=m\end{matrix}\right.\)
\(x^2_1+x^2_2=29\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\\ \Leftrightarrow7^2-2.m-29=0\\ \Leftrightarrow20-2m=0\\ \Rightarrow m=10\left(t/m\right)\)
Vậy \(m=10\)
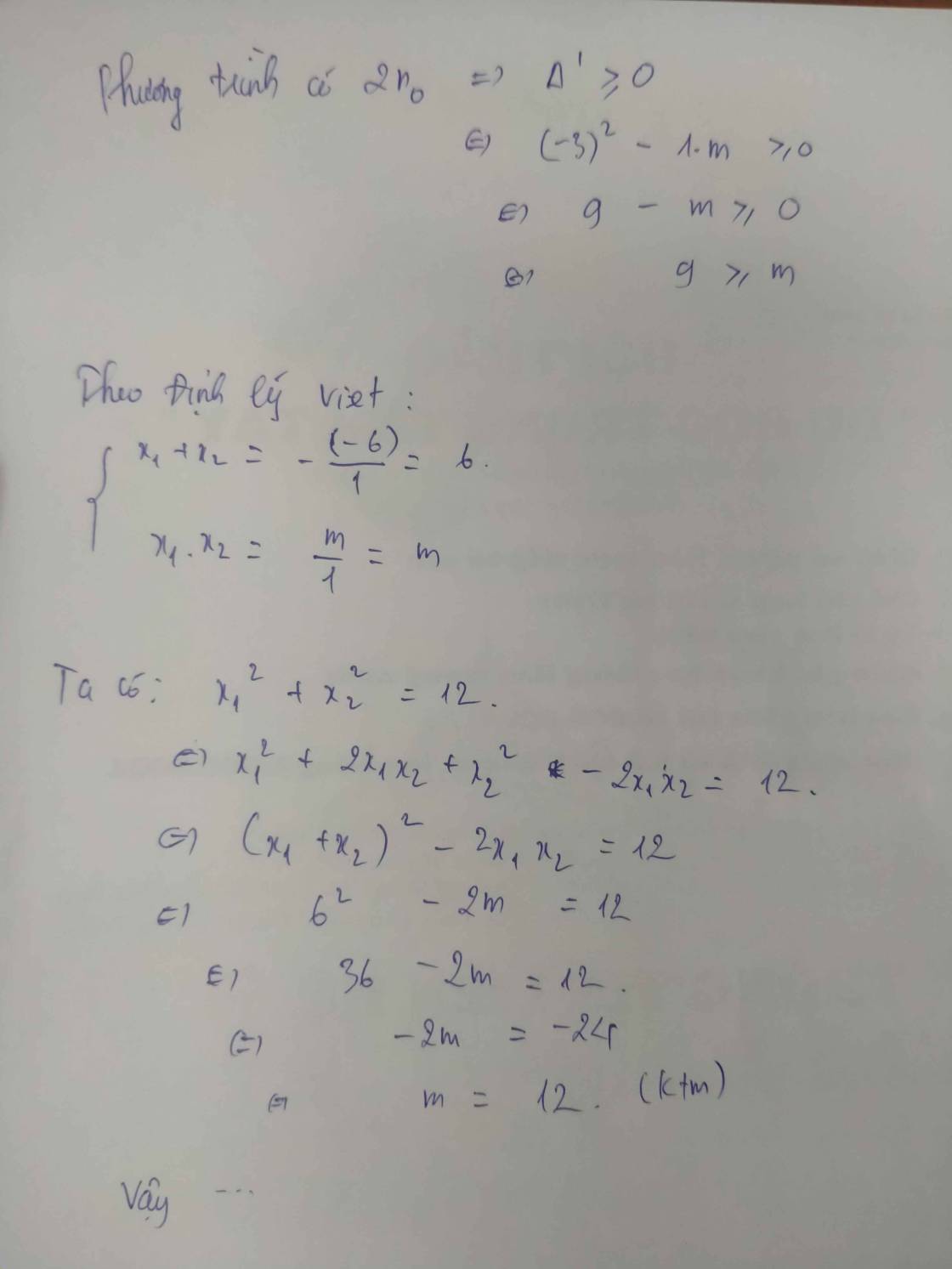
Ta có : x2 + 7x + 12 = 0
=> x2 + 4x + 3x + 12 = 0
=> x(x + 4) + 3(x + 4) = 0
=> (x + 3)(x + 4) = 0
=> \(\orbr{\begin{cases}x+3=0\\x+4=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-3\\x=-4\end{cases}}\)
Vậy \(x\in\left\{-3;-4\right\}\)
x2 + 7x + 12 = 0
<=> x2 + 3x + 4x + 12 = 0
<=> x( x + 3 ) + 4( x + 3 ) = 0
<=> ( x + 3 )( x + 4 ) = 0
<=> \(\orbr{\begin{cases}x+3=0\\x+4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-3\\x=-4\end{cases}}\)
Vậy S = { -3 ; -4 }