Cho tam giác ABC cân tại A, tanB=√2 a)Tính tỉ số lượng giác góc C b)kẻ AH vuông góc với BC, AH=2√3. Tính các cạnh của tam giác ABC Giúp em với ạ!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2021
\(tanB=\sqrt{2}\Rightarrow\dfrac{AC}{AB}=\sqrt{2}\Rightarrow\dfrac{AC^2}{AB^2}=2\)
\(\Rightarrow\dfrac{AC^2}{AB^2}+1=3\Rightarrow\dfrac{AC^2+AB^2}{AB^2}=3\Rightarrow\dfrac{BC^2}{AB^2}=3\)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{1}{\sqrt{3}}\)
Mà \(sinC=\dfrac{AB}{BC}\Rightarrow sinC=\dfrac{1}{\sqrt{3}}\)
\(sin^2C+cos^2C=1\Rightarrow\dfrac{1}{3}+cos^2C=1\Rightarrow cosC=\dfrac{\sqrt{6}}{3}\)
\(tanC=\dfrac{sinC}{cosC}=\dfrac{\sqrt{2}}{2}\)
b.
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AC=\dfrac{AH}{sinC}=\dfrac{2\sqrt{3}}{\dfrac{1}{\sqrt{3}}}=6\left(cm\right)\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AB=\dfrac{AC}{tanB}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)
Áp dụng Pitago:
\(BC=\sqrt{AB^2+AC^2}=3\sqrt{6}\left(cm\right)\)
14 tháng 7 2023
Bài 3 :
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)
14 tháng 4 2021
a, Xét tam giác ABC và tam giác HBA ta có :
^BAC = ^AHB = 900
^B _ chung
Vậy tam giác ABC ~ tam giác HBA ( g.g )
c, tam giác ABC vuông tại A, có đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=36+64=100\Rightarrow BC=10\)cm
Ta có : \(\dfrac{AC}{AH}=\dfrac{BC}{AB}\)( cặp tỉ số đồng dạng ý a )
\(\Rightarrow\dfrac{8}{AH}=\dfrac{10}{6}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}\)cm
d, phải là cắt AC nhé, xem lại đề nhé bạn
VD
11 tháng 3 2020
a) bạn tự vẽ hình nhé
sau khi kẻ, ta có AC=AH+HC=11
mà tam giác ABH vuông tại H
=> theo định lý Pytago => AH^2+BH^2=AB^2
=>BH=căn bậc 2 của 57
cũng theo định lý Pytago
=>BC^2=HC^2+BH^2
=>BC=căn bậc 2 của 66
VD
11 tháng 3 2020
b) bạn tự vẽ hình tiếp nha
ta có M là trung điểm của tam giác ABC => AM là đường trung tuyến của tam giác ABC vuông tại A
=>AM=MB=MC
theo định lý Pytago =>do tam giác HAM vuông tại H
=>HM^2+HA^2=AM^2
=>HM=9 => HB=MB-MH=32
=>AB^2=AH^2+HB^2 =>AB=căn bậc 2 của 2624
tương tự tính được AC=căn bậc 2 của 4100
=> AC/AB=5/4
CHÚC BẠN HỌC TỐT!!!
13 tháng 4 2023
a: góc B=góc C=(180-45)/2=67,5 độ
Vì góc A<góc B=góc C
nên BC<AB=AC
b: XetΔAHB vuông tại H và ΔAHC vuông tai H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
c: ΔABC cân tại A
mà AH là đường cao
nên AH là trung trực của BC
TN
23 tháng 4 2017
Hình tự vẽ
Xét \(\Delta MBH\)và \(\Delta NCH\)
\(\widehat{BMH}=\widehat{CNH}=90^o\)
\(BH=CH\left(cma\right)\)
\(\widehat{NBH}=\widehat{NQH}\)(Tam giác ABC cân tại A
\(\Rightarrow\Delta MBH=\Delta NCH\left(ch-gn\right)\)
\(MH=NH\left(2ctu\right)_{\left(1\right)}\)
Xét \(\Delta BQH\)và \(\Delta CNH\)
\(\widehat{Q}=\widehat{CNH}=90^o\)
\(BH=CH\left(cma\right)\)
\(\widehat{BHQ}=\widehat{NHC}\)(đối đỉnh)
\(\Rightarrow\Delta BQH=\Delta CNH\left(ch-gn\right)\)
\(\Rightarrow QH=NH\left(2ctu\right)_{\left(2\right)}\)
Từ \(\left(1\right),\left(2\right)\Rightarrow MH=QH\)
=> \(\Delta HQM\)cân tại H
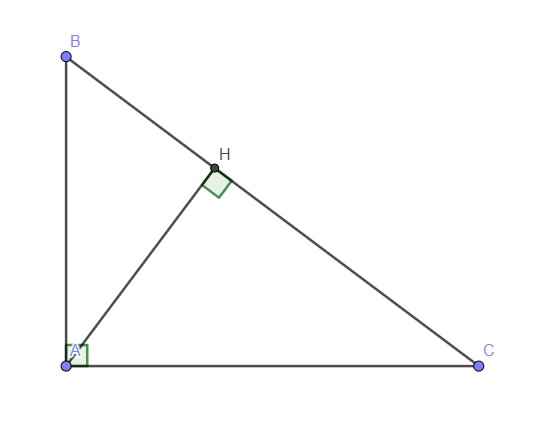
\(\tan B=\sqrt{2}\Leftrightarrow\dfrac{\sin B}{\cos B}=\sqrt{2}\Leftrightarrow\sin B=\sqrt{2}\cos B\\ \sin^2B+\cos^2B=1\Leftrightarrow3\cos^2B=1\\ \Leftrightarrow\cos B=\sqrt{\dfrac{1}{3}}=\dfrac{\sqrt{3}}{3}\\ \Leftrightarrow\sin B=\dfrac{\sqrt{6}}{3}\\ \Leftrightarrow\left\{{}\begin{matrix}\sin C=\cos B=\dfrac{\sqrt{3}}{3}\\\cos C=\sin B=\dfrac{\sqrt{6}}{3}\end{matrix}\right.\\ \cot C=\tan B=\sqrt{3};\tan C=\dfrac{1}{\cot C}=\dfrac{\sqrt{3}}{3}\)