trong hệ tọa độ Oxy, cho tam giác ABC có diện tích bằng \(36cm^2\) và trọng tâm \(G\left(4;2\right)\). Qua phép vị tự tâm \(I\left(1;-1\right)\), tỉ số k biến tam giác ABC thành tam giác A'B'C' có trọng tâm thuộc trục hoành. Tính diện tích tam giác A'B'C'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong hệ tọa độ Oxy, cho tam giác ABC có A(6; 1) ; B (-3; 5) và trọng tâm G(-1;1). Tìm tọa độ đỉnh C

Gọi C(x, y)
Vì G là trọng tâm tam giác ABC nên :
6 + − 3 + x 3 = − 1 1 + 5 + y 3 = 1 ⇔ x = − 6 y = − 3 .
Đáp án C

Vì M là trung điểm BC nên
x B = 2 x M − x C = 2.2 − − 2 = 6 y B = 2 y M − y C = 2.0 − − 4 = 4 ⇒ B 6 ; 4 .
Vì G là trọng tâm tam giác ABC nên
x A = 3 x G − x B − x C = − 4 y A = 3 y G − y B − y C = 12 → A − 4 ; 12 .
Suy ra x A + x B = ( − 4 ) + 6 = 2.
Đáp án B

Chọn A.
Gọi tọa độ điểm C( x ; y)
Vì O là trọng tâm tam giác ABC nên 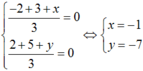

Tọa độ trọng tâm G x G ; y G là x G = 1 − 2 + 5 3 = 4 3 y G = 3 + 4 + 3 3 = 10 3 .
Chọn D.
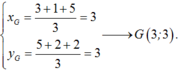
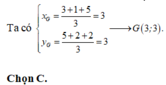


Gọi G' là trọng tâm tam giác A'B'C' thì G' là ảnh của G qua phép vị tự tâm I tỉ số k
Do G' thuộc trục hoàn nên tọa độ có dạng \(G'\left(a;0\right)\)
Áp dụng công thức tọa độ phép vị tự:
\(\left\{{}\begin{matrix}a-1=k\left(4-1\right)\\0+1=k\left(2+1\right)\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=3k+1\\k=\frac{1}{3}\end{matrix}\right.\)
\(\Rightarrow S_{A'B'C'}=\left|k\right|.S_{ABC}=\frac{1}{3}.36=12\)