chứng minh các đẳng thức sau 1/a(a+1) = 1/a trừ 1/a+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2021
Biến đổi tương đương:
\(\Leftrightarrow\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow a^2+b^2+2ab\ge4ab\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
VD
1
5 tháng 1 2021
\(\dfrac{1}{\sqrt{a}}< \sqrt{a+1}-\sqrt{a-1}\) <=> \(\left(\dfrac{1}{\sqrt{a}}\right)^2< \left(\sqrt{a+1}-\sqrt{a-1}\right)^2\)
<=> \(\dfrac{1}{a}< \left(a+1\right)+\left(a-1\right)-2\sqrt{a^2-1}\)
<=> \(2\sqrt{a^2-1}< 2a-\dfrac{1}{a}\)
<=> \(4\left(a^2-1\right)< 2\left(2a-\dfrac{1}{a}\right)^2\) <=> \(\dfrac{1}{a^2}>0\)
Vậy \(\dfrac{1}{\sqrt{a}}< \sqrt{a+1}-\sqrt{a-1}\) với mọi a ≥ 0=> đpcm.
HQ
1
AH
Akai Haruma
Giáo viên
21 tháng 12 2022
Lời giải:
\(a^{n+1}-1=(a^{n+1}-a^n)+(a^n-a^{n-1})+.....+(a-1)\)
\(=a^n(a-1)+a^{n-1}(a-1)+...+(a-1)=(a-1)(a^n+a^{n-1}+...+1)\)
Ta có đpcm.
BN
4 tháng 7 2023
a, \(VT=\dfrac{\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{ab}}.\left(\sqrt{a}-\sqrt{b}\right)=a-b=VP\) đpcm
b,\(VT=1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}-\dfrac{a^2-a}{a-1}=1-\sqrt{a}+\sqrt{a}-a=1-a=VP\) đpcm
CM
24 tháng 1 2019
a) Biến đổi vế trái:
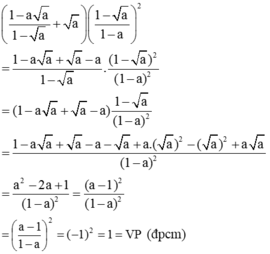
b) Biến đổi vế trái:
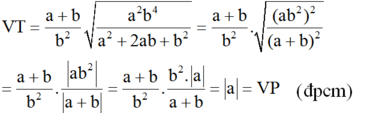
( v ì a + b > 0 n ê n | a + b | = a + b ; b 2 > 0 )
KV
23 tháng 10 2023
a) \(sin^4x+cos^4x=\left(sin^2x\right)^2+\left(cos^2x\right)^2\)
\(=\left(sin^2x\right)^2+2sin^2xcos^2x+\left(cos^2x\right)^2-2sin^2xcos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2xcos^2x\)
\(=1-2sin^2xcos^2x\)
b) \(\dfrac{1+cotx}{1-cotx}=\dfrac{tanx.cotx+cotx}{tanx.cotx-cotx}\)
\(=\dfrac{cotx.\left(tanx+1\right)}{cotx.\left(tanx-1\right)}\)
\(=\dfrac{tanx+1}{tanx-1}\)
c) \(\dfrac{cosx+sinx}{cos^3x}=\dfrac{1}{cos^2x}+\dfrac{tanx}{cos^2x}\)
\(=1+tan^2x+tanx.\dfrac{1}{cos^2x}\)
\(=1+tan^2x+tanx.\left(1+tan^2x\right)\)
\(=1+tan^2x+tanx+tan^3x\)
\(=tan^3x+tan^2x+tanx+1\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2023
Lời giải:
a.
$\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-2\sin ^2x\cos ^2x$
b.
$\frac{1+\cot x}{1-\cot x}=\frac{1+\frac{\cos x}{\sin x}}{1-\frac{\cos x}{\sin x}}=\frac{\cos x+\sin x}{\sin x-\cos x}(1)$
$\frac{\tan x+1}{\tan x-1}=\frac{\frac{\sin x}{\cos x}+1}{\frac{\sin x}{\cos x}-1}=\frac{\cos x+\sin x}{\sin x-\cos x}(2)$
Từ $(1); (2)$ ta có đpcm
c.
$\frac{\cos x+\sin x}{\cos ^3x}=(1+\frac{\sin x}{\cos x}).\frac{1}{\cos ^2x}$
$=(1+\tan x).\frac{\sin ^2x+\cos ^2x}{\cos ^2x}$
$=(1+\tan x)(\tan ^2x+1)=\tan ^3x+\tan ^2x+\tan x+1$
Ta có đpcm.
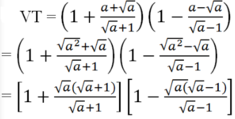
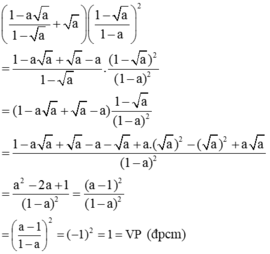
\(\frac{1}{a}-\frac{1}{a+1}=\frac{a+1}{a\left(a+1\right)}-\frac{a}{a\left(a+1\right)}=\frac{1}{a\left(a+1\right)}\)
Vậy \(\frac{1}{a\left(a+1\right)}=\frac{1}{a}-\frac{1}{a+1}\).
Đề bài: CM \(\frac{1}{a\left(a+1\right)}=\frac{1}{a}-\frac{1}{a+1}\)
Bài làm:
Ta có: \(\frac{1}{a\left(a+1\right)}=\frac{\left(a+1\right)-a}{a\left(a+1\right)}\)
\(=\frac{a+1}{a\left(a+1\right)}-\frac{a}{a\left(a+1\right)}\)
\(=\frac{1}{a}-\frac{1}{a+1}\)
=> \(\frac{1}{a\left(a+1\right)}=\frac{1}{a}-\frac{1}{a+1}\)
=> đpcm