Cho a,b là các số thực và \(0^o< \alpha< 90^o\). CMR: \(-\sqrt{a^2+b^2}\le a.\sin\alpha\le\sqrt{a^2+b^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:
\(\sin \alpha = \frac{{\sqrt 3 }}{2}\) với \(\alpha = {60^o}\) và \(\alpha = {120^o}\)
b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:
\(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\) với \(\alpha = {135^o}\)
c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\tan \alpha \) ta có:
\(\tan \alpha = - 1\) với \(\alpha = {135^o}\)
d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cot \alpha \) ta có:
\(\cot \alpha = - \sqrt 3 \) với \(\alpha = {150^o}\)

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:
\(\cos \alpha = \frac{{ - \sqrt 2 }}{2}\) với \(\alpha = {135^o}\)
b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:
\(\sin \alpha = 0\) với \(\alpha = {0^o}\) và \(\alpha = {180^o}\)
c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\tan \alpha \) ta có:
\(\tan \alpha = 1\) với \(\alpha = {45^o}\)
d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cot \alpha \) ta có:
\(\cot \alpha \) không xác định với \(\alpha = {0^o}\) hoặc \(\alpha = {180^o}\)

\(\left(a.cos\alpha+b.sin\alpha\right)^2\le\left(a^2+b^2\right)\left(sin^2a+cos^2a\right)=a^2+b^2\)
\(\Rightarrow-\sqrt{a^2+b^2}\le a.cos\alpha+b.sin\alpha\le\sqrt{a^2+b^2}\)

a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
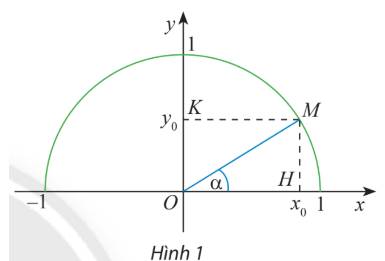
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)

Cách 1:
Ta có: \(tan\alpha=\sqrt{2}\Rightarrow\left\{{}\begin{matrix}\dfrac{sin\alpha}{cos\alpha}=\sqrt{2}\\1+\left(\sqrt{2}\right)^2=\dfrac{1}{cos^2\alpha}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sin\alpha=\sqrt{2}\cdot cos\alpha\\cos^2\alpha=\dfrac{1}{3}\end{matrix}\right.\)
\(P=\dfrac{sin\alpha-cos\alpha}{sin^3\alpha+3cos^3\alpha+2sin\alpha}\)
\(=\dfrac{\sqrt{2}\cdot cos\alpha-cos\alpha}{\left(\sqrt{2}\cdot cos\alpha\right)^3+3cos^3\alpha+2\cdot\sqrt{2}\cdot cos\alpha}\)
\(=\dfrac{cos\alpha\left(\sqrt{2}-1\right)}{2\sqrt{2}\cdot cos^3\alpha+3cos^3\alpha+2\sqrt{2}\cdot cos\alpha}\)
\(=\dfrac{cos\alpha\left(\sqrt{2}-1\right)}{cos\alpha\left(2\sqrt{2}\cdot cos^2\alpha+3cos^2\alpha+2\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{2}-1}{2\sqrt{2}\cdot cos^2\alpha+3cos^2\alpha+2\sqrt{2}}\)
Thay \(cos^2\alpha=\dfrac{1}{3}\) vào \(P\) ta có:
\(P=\dfrac{\sqrt{2}-1}{2\sqrt{2}\cdot\dfrac{1}{3}+3\cdot\dfrac{1}{3}+2\sqrt{2}}=\dfrac{\sqrt{2}-1}{1+\dfrac{8}{3}\sqrt{2}}\)
\(=\dfrac{3\left(\sqrt{2}-1\right)}{3\left(1+\dfrac{8}{3}\sqrt{2}\right)}=\dfrac{3\left(\sqrt{2}-1\right)}{3+8\sqrt{2}}\)
\(=\dfrac{3\left(\sqrt{2}-1\right)}{3+2^3\sqrt{2}}=\dfrac{a\left(\sqrt{b}-1\right)}{a+b^3\sqrt{b}}\)
\(\Rightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\Rightarrow a+b=5\)
Chọn đáp án A.
Cách 2:
\(P=\dfrac{sin\alpha-cos\alpha}{sin^3\alpha+3cos^3\alpha+2sin\alpha}=\dfrac{\left(sin\alpha-cos\alpha\right)\div cos^3\alpha}{\left(sin^3\alpha+3cos^3\alpha+2sin\alpha\right)\div cos^3\alpha}\)
\(=\dfrac{\dfrac{sin\alpha}{cos^3\alpha}-\dfrac{1}{cos^2\alpha}}{\dfrac{sin^3\alpha}{cos^3\alpha}+3+2\cdot\dfrac{sin\alpha}{cos^3\alpha}}=\dfrac{\dfrac{sin\alpha}{cos\alpha}\cdot\dfrac{1}{cos^2\alpha}-\dfrac{1}{cos^2\alpha}}{tan^3\alpha+3+2\cdot\dfrac{sin\alpha}{cos\alpha}\cdot\dfrac{1}{cos^2\alpha}}\)
\(=\dfrac{tan\alpha\cdot\left(1+tan^2\alpha\right)-\left(1+tan^2\alpha\right)}{tan^3\alpha+3+2tan\alpha\cdot\left(1+tan^2\alpha\right)}\)
Thay \(tan\alpha=\sqrt{2}\) vào ta có:
\(P=\dfrac{\sqrt{2}\cdot\left[1+\left(\sqrt{2}\right)^2\right]-\left[1+\left(\sqrt{2}\right)^2\right]}{\left(\sqrt{2}\right)^3+3+2\sqrt{2}\cdot\left[1+\left(\sqrt{2}\right)^2\right]}=\dfrac{3\sqrt{2}-3}{2\sqrt{2}+3+6\sqrt{2}}\)
\(=\dfrac{3\left(\sqrt{2}-1\right)}{3+8\sqrt{2}}=\dfrac{3\left(\sqrt{2}-1\right)}{3+2^3\sqrt{2}}=\dfrac{a\left(\sqrt{b}-1\right)}{a+b^3\sqrt{b}}\)
\(\Rightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\Rightarrow a+b=3+2=5\)
Chọn đáp án A

a/ \(\frac{\pi}{2}\le y\le\pi\Rightarrow cosy< 0\)
\(\Rightarrow cosy=-\sqrt{1-sin^2y}=-\frac{2\sqrt{2}}{3}\)
\(sin2y=2siny.cosy=2.\left(\frac{1}{3}\right).\left(-\frac{2\sqrt{2}}{3}\right)=-\frac{4\sqrt{2}}{9}\)
\(cos\left(\frac{\pi}{3}-y\right)=cos\frac{\pi}{3}cosy+sin\frac{\pi}{3}siny=\frac{\sqrt{3}-2\sqrt{2}}{6}\)
\(tany+5=\frac{siny}{cosy}+5=5-\frac{\sqrt{2}}{4}\)
b/ \(-\frac{\pi}{2}\le a\le9\Rightarrow sina\le0\)
\(\Rightarrow sina=\sqrt{1-cos^2a}=-\frac{4}{5}\)
\(sin2a=2sina.cosa=-\frac{24}{25}\)
\(cos2a=cos^2a-sin^2a=-\frac{7}{25}\)
\(tan2a=\frac{sin2a}{cos2a}=\frac{24}{7}\)
c/ \(\pi\le a\le\frac{3\pi}{2}\Rightarrow\left\{{}\begin{matrix}sina\le0\\cosa\le0\end{matrix}\right.\)
\(\Rightarrow cosa=-\frac{1}{\sqrt{1+tan^2a}}=-\frac{1}{2}\Rightarrow sina=-\frac{\sqrt{3}}{2}\)
\(\Rightarrow sin2a=2sina.cosa=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\left(\sqrt{3}-sin2a\right)sin\frac{2\pi}{3}=\frac{3}{4}\)

a)
\(\begin{array}{l}\sin {168^o}45'33'' = 0,195;\\\cos {17^o}22'35'' = 0,954;\\\tan {156^o}26'39'' = - 0,436;\\\cot {56^o}36'42'' = 0,659\end{array}\)
b)
i) \(\alpha = {59^o}32'30,8''.\)
ii) \(\alpha = {124^o}32'28,65''.\)
iii) \(\alpha = {18^o}28'9,55''.\)
mình nghĩ nên sửa đề là \(-\sqrt{a^2+b^2}\le a\cos\alpha+b\sin\alpha\le\sqrt{a^2+b^2}\)
với a,b,x,y là số thực ta luôn có \(\left(ax+by\right)^2=\left(a^2+b^2\right)\left(x^2+y^2\right)-\left(ay-bx\right)^2\)
từ đẳng thức này ta suy ra \(\left(ax+by\right)^2\le\left(a^2+b^2\right)\left(x^2+y^2\right)\)
dấu "=" xảy ra khi \(\left(ax-by\right)^2=0\)
trở lại bài toán ta luôn có \(\left(a\cos\alpha+b\sin\alpha\right)^2\le\left(a^2+b^2\right)\left(\cos^2\alpha+\sin^2\alpha\right)=a^2+b^2\)
từ đó ta có \(-\sqrt{a^2+b^2}\le a\cos\alpha+b\sin\alpha\le\sqrt{a^2+b^2}\)