Một quả cầu nặng m=100g được treo ở đầu một sợi dây nhẹ, không co dãn, dài l=1m (đầu kia của dây cố định). Truyền cho quả cầu ở vị trí cân bằng một vận tốc đầu v0 theo phương ngang. Khi dây treo nghiêng góc α =30o so với phương thẳng đứng thì gia tốc của quả cầu có phương ngang. Cho g=10m/s2, bỏ qua mọi ma sát.
a) Tìm vận tốc v0.
b) Tính lực căng dây và vận tốc của vật tại vị trí có góc lệch a = 40o.


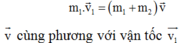
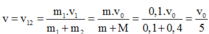
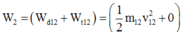

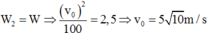

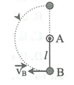
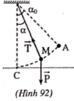
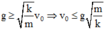

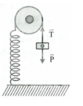
a) Khi dây treo nghiêng góc α=300 so với phương thẳng đứng, vật M chịu tác dụng của các lựcnhư hình vẽ. Do gia tốc có phương ngang nên:\(T.\cos30^0=mg\) (1)
(1)
Mặt khác, xét theo phương hướng tâm MO ta có:
Từ (1) và (2) suy ra:\(v^2=\frac{gl}{2\sqrt{3}}\) (3)
(3)
Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí M và khi vật ở vị trí cân bằng ta được:
v02=v2+2gl(1 – cos300) = \(\frac{12-5\sqrt{3}}{6}gl\rightarrow\)v0 ≈ 2,36m/s
\(\frac{12-5\sqrt{3}}{6}gl\rightarrow\)v0 ≈ 2,36m/s
b) Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí \(\alpha\)=40o và khi vật ở vị trí cân bằng ta được:
Xét theo phương sợi dây ta có:
\(T=mgcos40^0+\frac{mv^2}{l}=0,1.10.cos40^0+\frac{0,1.0,94^2}{1}=0,86\left(N\right)\)