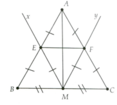
Cho tam giác ABC, vẽ đường cao AH. Lấy E và F sao cho AB là trung trực của HE, AC là trung trực của HF.Nối E với F cắt AB tại M , cắt AC tại N. CMR : MN song song với EH, NB song song với FH.
(Ai giải nhanh nhất mình sẽ tick)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
15 tháng 4 2017
b)Vì AC là trung trực của HF (gt)
=>AC vuông góc với HF (ĐN)
IH=IF (ĐN)
Vì tam giác MSE=tam giác MSH ( CM câu a) =>ME=MH ( 2 cạnh tương ứng)
Xét tam giác AES vuông tại S và tam giác ASH vuông tại S có:
Chung SA
SE=SH ( CM câu a)
=>Tam giác AES=tam giác ASH ( 2 cạnh góc vuông)
=> AE=AH ( 2 cạnh tương ứng)
Xét tam giác AME và tam giác AMH có
AE=AH ( CM trên)
Chung AM
ME=MH ( CM trên)
=> Tam giác AME= tam giác AMH ( cạnh-cạnh- cạnh)
=>^AEM=^AHM ( 2 góc tương ứng) (1)
Xét tam giác NHI vuông tại I và tam giác NFI vuông tại I có:
Chung NI
IH=IF ( CM trên)
=> Tam giác NHI= tam giác NGI ( 2 cạnh góc vuông)
=> NH=NF ( 2 cạnh tương ứng)
Xét tam giác AHI vuông tại I và tam giác AFI vuông tại I có:
Chung AI
IH=IF ( CM trên)
=> Tam giác AHI= tam giác AFI ( 2 cạnh góc vuông)
=> AH=AF( 2 cạnh tương ứng)
LT
14 tháng 4 2017
a)Gọi HE cắt AB tại S, HE cắt AC tại I
Vì AB là đường trung trực HE(gt)
=>AB vuông góc với HE ( ĐN)
SE=SH ( ĐN)
Xét tam giác MSE vuông tại S và tam giác MSH vuông tại H có:
Chung MS
SE=SH ( CM trên)
=> Tam giác MSE=Tam giác MSH ( 2 cạnh góc vuông)
=> ^EMB=^BMH, mà tia MB nằm giữa hai tia ME,MH
=> MB là tia phân giác ^EMH
25 tháng 6 2017
Do \(AB\) là trung trực của \(HD\) nên \(AH\) nên \(AH=AD\) . Từ đó suy ra \(AB\) là phân giác góc \(DAH\) . Vậy góc \(A_1=A_2\) . Tương tự \(A_3=A_4\)
Từ đó suy ra \(A_2+A_4=A_1+A_3=90^o\)
Vậy góc \(A_1+A_2+A_3+A_4=180^o\)
Chẳng biết đúng hay sai mới chuần bị lên lớp 6
CM
29 tháng 12 2018
a) Mx đi qua trung điểm M của BC và song song với AC. Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC. Khi đó EF trở thành đường trung bình của tam giác ABC;
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF. Suy ra AM là đường trung trực của EF.
