Cho tam giâc ABC nhọn có các đường cao AD BE CF cắt nhau tại H cho biết tanABC + tanACB = 2tanBAC.Tính tanACB tanABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


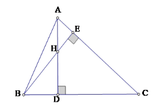
Xét tam giác vuông ABD và ADC, ta có tan B = A D B D ; tan C = A D C D
Suy ra: tan B . tan C = A D 2 B D . C D (1)
Lại có: H B D ^ = C A D ^ (cùng phụ với A C B ^ ) và H D B ^ = A D C ^ = 90 0
Do đó ∆ B D H ~ ∆ A D C (g.g), suy ra D H D C = B D A D , do đó BD.DC = DH.AD (2)
Từ (1) và (2) suy ra tan B . tan C = A D 2 D H . A D = A D D H (3)
Theo giả thiết H D A H = 1 2 suy ra H D A H + H D = 1 2 + 1 hay H D A D = 1 3 , suy ra AD = 3HD
Thay vào (3) ta được: tan B . tan C = 3 H D D H = 3
Đáp án cần chọn là: B

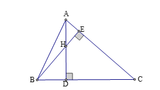
Xét tam giác vuông ABD và ADC, ta có: tan B = A D B D ; tan C = A D C D
Suy ra: tan B . tan C = A D 2 B D . C D (1)
Lại có H B D ^ = C A D ^ (cùng phụ với A C B ^ ) và H D B ^ = A D C ^ = 90 0
Do đó ∆ B D H ~ ∆ A D C (g.g), suy ra D H D C = B D A D , do đó BD.DC = DH.AD (2)
Từ (1) và (2) suy ra tan B . tan C = A D 2 D H . A D = A D D H (3)
Theo giả thiết H D A H = 3 2 suy ra H D A H + H D = 3 2 + 3 hay H D A D = 3 5 , suy ra AD = 5 3 HD
Thay vào (3) ta được: tan B . tan C = 5 3 H D D H = 5 3
Đáp án cần chọn là: D

b: góc HID+góc HKD=180 độ
=>HIDK nội tiếp
=>góc HIK=góc HDK
=>góc HIK=góc HCB
=>góc HIK=góc HEF
=>EF//IK



-Xét △BCF và △BAD có:
\(\widehat{ABC}\) là góc chung
\(\widehat{BFC}=\widehat{BDA}=90^0\)
\(\Rightarrow\)△BCF∼△BAD (g-g).
\(\Rightarrow\dfrac{BC}{BA}=\dfrac{BF}{BD}\) (tỉ số đồng dạng)
\(\Rightarrow BF.BA=BC.BD\left(1\right)\)
-Xét △ACD và △BCE có:
\(\widehat{ACB}\) là góc chung
\(\widehat{ADC}=\widehat{BEC}=90^0\)
\(\Rightarrow\)△ACD∼△BCE (g-g)
\(\Rightarrow\dfrac{AC}{BC}=\dfrac{CD}{CE}\) (tỉ số đồng dạng)
\(\Rightarrow CE.CA=CD.BC\left(2\right)\)
-Từ (1) và (2) suy ra:
\(BF.BA+CE.CA=BD.BC+CD.BC=BC\left(BD+CD\right)=BC.BC=BC^2\)