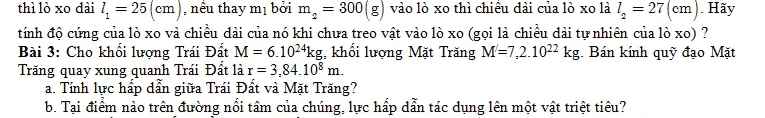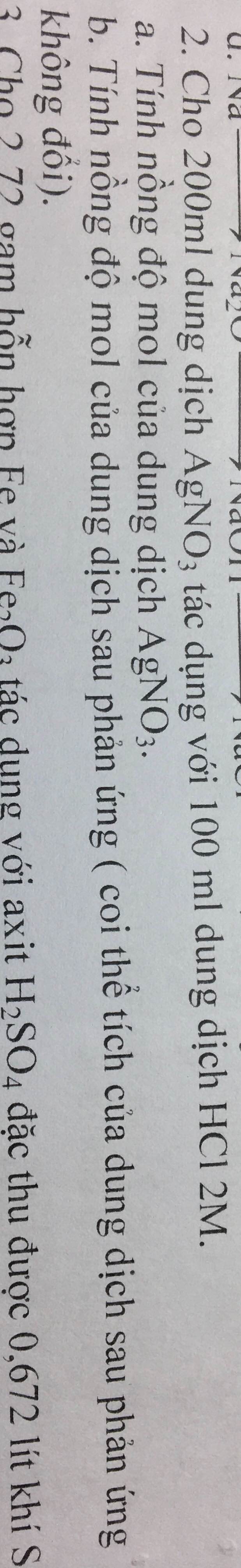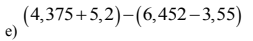Giải giúp mình với, cảm ơn mọi người ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
TK
9 tháng 12 2021
Bài 3:
a, Lực hấp dẫn giữa Trái Đất và Mặt Trăng
\(F_{hd}=G\cdot\dfrac{M_1M_2}{r^2}=6,67\cdot10^{-11}\cdot\dfrac{6\cdot10^{24}\cdot7,2\cdot10^{22}}{\left(3,84\cdot10^8\right)^2}=1,95\cdot10^{20}\left(N\right)\)
NH
1
2 tháng 12 2021
Bài 3.
Định luật ll Niu-tơn:
\(\overrightarrow{F}+\overrightarrow{F_{ms}}=m\cdot\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m\cdot a\)
Gia tốc vật:
\(a=\dfrac{F-F_{ms}}{m}=\dfrac{4,5-\mu mg}{m}=\dfrac{4,5-0,2\cdot1,5\cdot10}{1,5}=1\)m/s2
Vận tốc vật sau 2s:
\(v=a\cdot t=1\cdot2=2\)m/s
NC
1
LP
1
HP
30 tháng 10 2021
Đổi 100ml = 0,1 lít
Ta có: \(n_{HCl}=2.0,1=0,2\left(mol\right)\)
a. PTHH: \(AgNO_3+HCl--->AgCl\downarrow+HNO_3\)
Theo PT: \(n_{AgNO_3}=n_{HCl}=0,2\left(mol\right)\)
Đổi 200ml = 0,2 lít
=> \(C_{M_{AgNO_3}}=\dfrac{0,2}{0,2}=1M\)
b. Ta có: \(m_{dd_{HNO_3}}=0,1\left(lít\right)\)
Theo PT: \(n_{HNO_3}=n_{HCl}=0,2\left(mol\right)\)
=> \(C_{M_{HNO_3}}=\dfrac{0,2}{0,1}=2M\)
KS
2 tháng 5 2022
(`4,375` + `5,2` ) - ( `6,452` - `3,55` )
= `9,575 - `2,902`
=`6,673`
PB
0
21 tháng 7 2021
a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=\dfrac{81}{4}+36=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\dfrac{81}{4}}{\dfrac{15}{2}}=\dfrac{27}{10}\)cm
=> \(CH=BC-BH=\dfrac{15}{2}-\dfrac{27}{10}=\dfrac{24}{5}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}\)
\(=\dfrac{4,5.6}{\dfrac{15}{2}}=\dfrac{18}{5}\)cm
AT
21 tháng 7 2021
tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow BC^2=AB^2+AC^2=\left(4,5\right)^2+6^2=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}=7,5\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\left(4,5\right)^2}{7,5}=\dfrac{27}{10}=2,7\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{6^2}{7,5}=\dfrac{24}{5}=4,8\left(cm\right)\)
HK
1
