cho hình thang cân ABCD ( AB // CD).Gọi E,I ,K,M lần lượt là trung điểm của các cạnh AB,BC,CD,DA
a) Tứ giác EIKM là hình j ? Vì sao?
b) chứng minh tam giác DEC cân
c) hình thang ABCD cần thêm điều kiện gì để tứ giác IKME là hình vuông
d) trong điều kiện cua câu c, nếu BD=8cm.tính iện tích EIKM

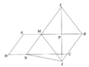
Xét \(\Delta\)ABC có: E, I là trung điểm AB, BC
\(\Rightarrow\) EI là đường trung bình tam giác ABC
\(\Rightarrow\) EI//AC, EI=1/2AC
Chứng minh tương tự: MK//AC, MK=1/2AC
\(\Rightarrow\) EI//MK, EI=MK
\(\Rightarrow\) tứ giác EIKM là hình bình hành (1)
ta có: EA=EB, \(\widehat{A}\)=\(\widehat{B}\), BI=MA(do AD=BC)
\(\Rightarrow\) \(\Delta\)AEM=\(\Delta\)BEI
\(\Rightarrow\) EM=EI(2)
Từ (1), (2)
\(\Rightarrow\) tứ giác EIKM là hình thoi
Để hình thoi EIKM là hình vuông thì EM\(\perp\)EI
\(\Rightarrow\) AC⊥BD
\(\Rightarrow\) hình thang ABCD có 2 đường chéo vuông góc với nhau
Vậy hình thang ABCD có đường chéo vuông góc với nhau thì EIKM là hình vuông.
#Shinobu Cừu