Ví dụ 5: Cho a, b \(\inℤ\)và b > 0. So sánh hai số hữu tỉ \(\frac{a}{b}\)và \(\frac{a+1}{b+1}\)
Ví dụ 6: Đồng bạch là 1 loại kim hợp có niken, kẽm và đồng, khối lượng của chúng tỉ lệ với các số 3;4;13. Hỏi cần bao nhiêu kilogam niken, kẽm và đồng để sản xuất ra được 150kg đồng bạch ?

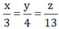 .
.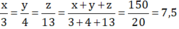 .
.
Vì dụ 5: Để so sánh \(\frac{a}{b}\)và \(\frac{a+1}{b+1}\) , ta đi so sánh giữa 2 số a (b+1) và b(a+1) .
Xét hiệu: a(b+1) - b(a+1) = ab+ a - (ab +b) = a-b. Ta có 3 trường hợp, với điều kiện b >0:
Trường hợp 1: Nếu a-b = 0 \(\Leftrightarrow\)a = b thì :
a(b+1) - b(a+1) = 0\(\Leftrightarrow\)a(b+1) = b(a+1)
\(\Leftrightarrow\)\(\frac{a\left(b+1\right)}{b\left(b+1\right)}\)= \(\frac{b\left(a+1\right)}{b\left(b+1\right)}\)\(\Leftrightarrow\frac{a}{b}\)=\(\frac{a+1}{b+1}\).
Trường hợp 2: Nếu a - b< 0 \(\Leftrightarrow\)a < b thì:
a(b+1) - b(a+1)< 0\(\Leftrightarrow\)a(b+1) < b(a+1)
\(\Leftrightarrow\)\(\frac{a\left(b+1\right)}{b\left(b+1\right)}\)< \(\frac{b\left(a+1\right)}{b\left(b+1\right)}\)\(\Leftrightarrow\)\(\frac{a}{b}\)< \(\frac{a+1}{b+1}\).
Trường hợp 3: Nếu a-b> 0 \(\Leftrightarrow\) a > b thì:
a(b+1) - b(a+1) > 0 \(\Leftrightarrow\)a(b+1) > b(a+1)
\(\Leftrightarrow\frac{a\left(b+1\right)}{b\left(b+1\right)}\)>\(\frac{b\left(a+1\right)}{b\left(b+1\right)}\)\(\Leftrightarrow\frac{a}{b}\)>\(\frac{a+1}{b+1}\).
Ví dụ 6: Bg: Gọi khối lượng của niken, kẽm và đồng theo thứ tự m1, m2, m3. Từ giả thiết ta có: m1+m2+m3 = 150 kg.
\(\frac{m_1}{3}\) =\(\frac{m_2}{4}=\frac{m_3}{13}\Rightarrow\frac{m_1}{3}=\frac{m_2}{4}=\frac{m_3}{13}=\)\(\frac{m_1+m_2+m_3}{3+4+13}=\frac{150}{20}=7,5\)
Từ đó, suy ra m1 = 3.7,5 = 22,5kg, m2 = 4.7,5 = 30 kg và m3 = 13.7,5 = 97,5kg .