Cho tam giác ABC vuông tại A.Biết góc B=50° a,Tính số đo góc C b,Tia phân giác của góc B cắt AC tại D.Trên cạnh BC lấy điểm E sao cho BE=BA Chứng minh:∆ABD=∆EBD c,Chứng minh:DE vuông góc với BC d,Gọi K là giao điểm của 2 đường thẳng AB và DE.Chứng minh:DK=DC,AK=EC e,Chứng mjnh: BDvuông góc vớiCK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

YN
22 tháng 12 2021
Answer:
Phần c) thì nhờ các cao nhân khác thoii.
a) Ta xét tam giác ABD và tam giác EBD:
AB = EB (gt)
BD cạnh chung
\(\widehat{B_1}=\widehat{B_2}\)
Vậy tam giác ABD = tam giác EBD (c.g.c)
\(\Rightarrow DE=DA\)
b) Theo phần a), tam giác ABD = tam giác EBD
\(\Rightarrow\widehat{BAD}=\widehat{BED}=90^o\)

17 tháng 12 2020
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
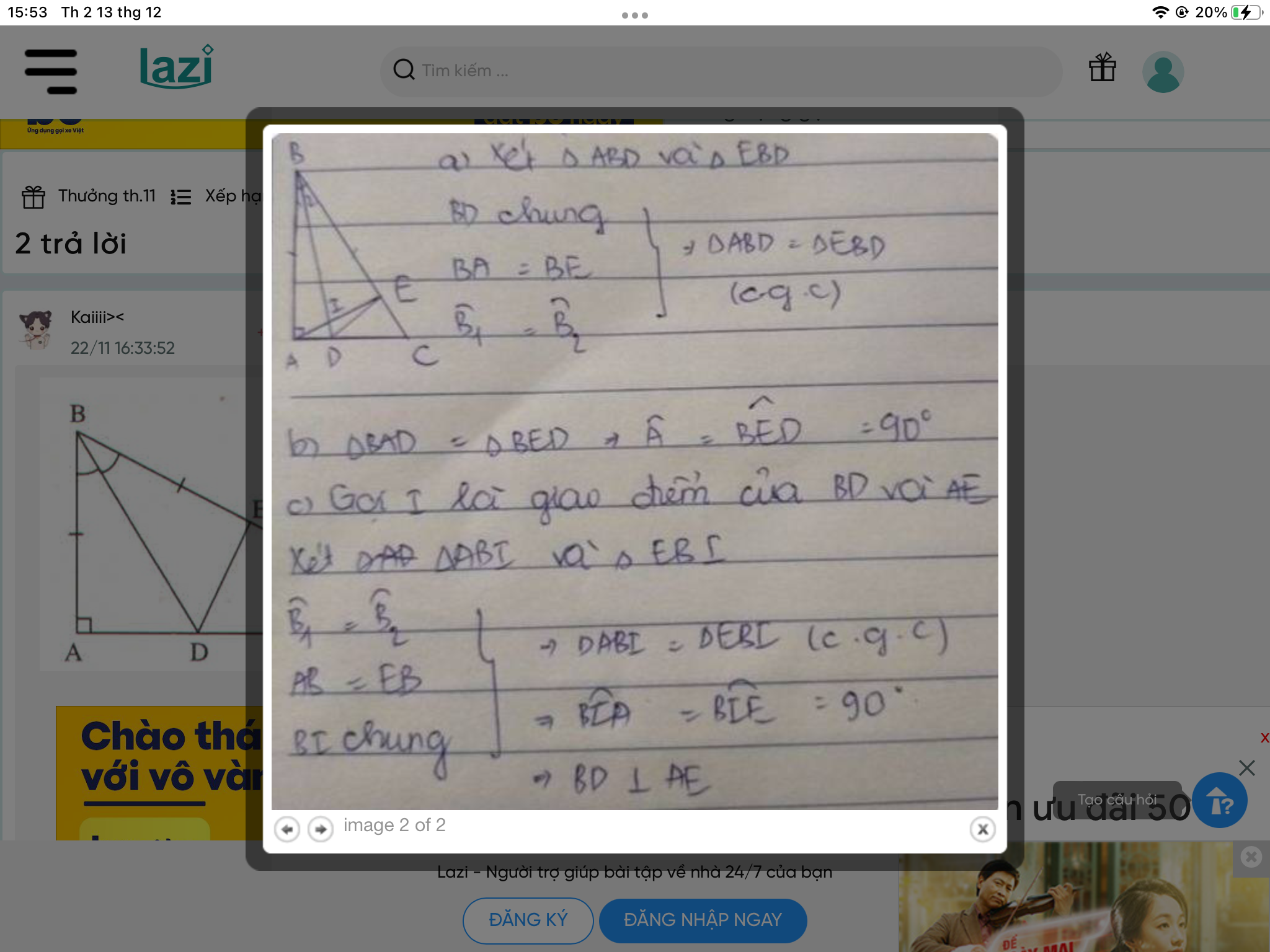
a)
Ta có: góc B + góc C = 90 độ
Mà góc B = 50 độ
\(\Rightarrow\) góc C = 90 độ - 50 độ = 40 độ
b)
Xét Δ ABD và Δ EBD có:
AB = EB (gt)
góc ABD = góc EBD (gt)
chung BD
\(\Rightarrow\) Δ ABD = Δ EBD (c-g-c)
c)
Vì Δ ABD = Δ EBD (câu b)
\(\Rightarrow\) góc BAD = góc BED
Mà góc BAD = 90 độ nên góc BED = 90 độ
\(\Rightarrow\)DE \(\perp\) BC
d)
Vì Δ ABD = Δ EBD (câu b)
\(\Rightarrow\) AD = ED
Xét Δ ADK và Δ EDC có:
góc DAK = góc DEC = 90 độ
AD = ED (cmt)
góc ADK = góc EDC (đ²)
\(\Rightarrow\) Δ ADK = Δ EDC (cgv - gn)
\(\Rightarrow\) DK = DC và AK = EC ( 2 cạnh tương ứng )
e)
Ta có:
BA = BE (gt)
AK = EC (câu d)
\(\Rightarrow\) BA + AK = BE + EC \(\Rightarrow\) BK = BC \(\Leftrightarrow\) Δ BKC cân tại B (định nghĩa)
Mà BD là phân giác góc CBK
\(\Rightarrow\) BD vừa là phân giác vừa là đường cao của Δ BKC
\(\Rightarrow\) BD ⊥ CK
#Tiểu Cừu
a) XÉT \(\Delta ABD\)VÀ \(\Delta EBD\)CÓ
BD LÀ CẠNH CHUNG
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
AB = BE (GT)
=> \(\Delta ABD\)=\(\Delta EBD\)(C-G-C)
C) VÌ \(\Delta ABD\)=\(\Delta EBD\)(CMT)
=> \(\widehat{BAD}=\widehat{BED}=90^o\)
=> DE VUÔNG GÓC VỚI BC (ĐPCM )
D) vì \(\Delta ABD\)=\(\Delta EBD\)(CMT )
=> AD = ED ( HAI CẠNH TƯƠNG ỨNG )
XÉT \(\Delta ADK\)VÀ \(\Delta EDC\)CÓ
\(\widehat{KAD}=\widehat{CED}=90^o\)
AD = ED (CMT)
\(\widehat{ADK}=\widehat{EDC}\left(Đ^2\right)\)
=> \(\Delta ADK\)=\(\Delta ADK\)(G-C-G)
=> DK = DC (ĐPCM)
=> AK = EC (ĐPCM)
e ) vì \(\Delta ABD\)=\(\Delta EBD\)(CMT)
=>\(\widehat{ADB}=\widehat{EDB}\)
TA CÓ
\(\widehat{ADB}=\widehat{D_1}\)(ĐỐI DỈNH)
\(\widehat{EDB}=\widehat{D_2}\)(ĐỐI ĐỈNH)
MÀ \(\widehat{ADB}=\widehat{EDB}\)
=> \(\widehat{D_1}=\widehat{D_2}\)
GỌI O LÀ GIAO ĐIỂM CỦA BD LÀ KC
XÉT \(\Delta KDO\)VÀ \(\Delta CDO\)CÓ
\(KD=CD\left(cmt\right)\)
\(\widehat{D_1}=\widehat{D_2}\)(CMT)
DO LÀ CẠNH CHUNG
=> \(\Delta KDO\)=\(\Delta CDO\)(C-G-C)
=> \(\widehat{KOD}=\widehat{COD}\)
MÀ HAI GÓC NÀY KỀ BÙ
\(\Rightarrow\widehat{KOD}=\widehat{COD}=\frac{180^o}{2}=90^o\)
\(\Rightarrow BD\perp CK\left(đpcm\right)\)