Cho y=a sinx + b cosx + x. Tìm điều kiện về a,b để hàm số đồng biến trên R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 8 2017
y ' = 1 + m cos x - sin x = 1 - 2 m sin x - π 4
Đặt t = sin x - π 4 với t ∈ - 1 ; 1 ta có f 1 = 1 - 2 m t
Để hàm số đồng biến trên R thì
f t ≥ 0 ∀ t ∈ - 1 ; 1 ⇔ f - 1 ≥ 0 f 1 ≥ 0 ⇔ 1 + 2 m ≥ 0 1 - 2 m ≥ 0
⇔ m ≥ - 2 2 m ≤ 2 2 ⇔ - 2 2 ≤ m ≤ 2 2
Đáp án A
.
.
.
.
.
.
.
, 
.
.
30 tháng 5 2021
C1: \(a.sinx+b.cosx=c\)
Pt vô nghiệm \(\Leftrightarrow a^2+b^2< c^2\)
Bạn áp dụng công thức trên sẽ tìm ra m
C2: (Bạn vẽ đường tròn lượng giác sẽ tìm được)
Hàm số \(y=sinx\) đồng biến trên khoảng \(\left(-\dfrac{\pi}{2}+k2\pi;\dfrac{\pi}{2}+k2\pi\right)\) ( góc phần tư thứ IV và I)
Hàm nghịch biến trên khoảng \(\left(\dfrac{\pi}{2}+k2\pi;\dfrac{3\pi}{2}+k2\pi\right)\)( góc phần tư thứ II và III)
Ý A, khoảng nằm trong góc phần tư thứ III và thứ IV => Hàm nghịch biến sau đó đồng biến
Ý B, khoảng nằm trong góc phần tư thứ I và thứ II => hàm đồng biến sau đó nghịch biến
Ý C, khoảng nằm trong góc phần tư thứ IV; I ; II => hàm đồng biền sau đó nghịch biến
Ý D, khoảng nằm trong phần tư thứ IV ; I=> hàm đồng biến
Đ/A: Ý D
(Toi nghĩ thế)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
a.
Hàm là hàm số bậc nhất khi:
\(2m-1\ne0\Leftrightarrow m\ne\dfrac{1}{2}\)
b.
Hàm đồng biến trên R khi:
\(2m-1>0\Leftrightarrow m>\dfrac{1}{2}\)
30 tháng 7 2021
a) Để hàm số là hàm số bậc nhất thì \(2m-1\ne0\)
hay \(m\ne\dfrac{1}{2}\)
b) Để hàm số đồng biến thì 2m-1>0
hay \(m>\dfrac{1}{2}\)
CM
18 tháng 8 2018
Đáp án A
Ta có: 
Hàm số đồng biến trên R khi 
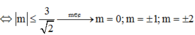
Vậy có 5 giá trị nguyên của m
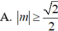
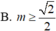
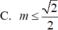
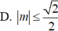
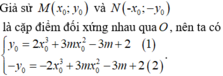
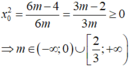
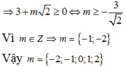
Ta có: \(y'=a\)\(cosx-b\)\(sinx+1\)
y đồng biến trên R \(\Leftrightarrow y'\ge0,\forall x\in R\)
\(\Leftrightarrow acosx-bsinx+1\ge0,\forall x\in R\)(*)
Theo bất đẳng thức Schwartz thì:
\(|acosx-bsinx|\le\sqrt{a^2+b^2},\forall x\)
\(\Leftrightarrow-\sqrt{a^2+b^2}\le acos-bsinx\le\sqrt{a^2+b^2},\forall x\)
\(\Leftrightarrow1-\sqrt{a^2+b^2}\le acos-bsinx+1\le1+\sqrt{a^2+b^2},\forall x\)
Do đó (*) \(\Leftrightarrow1-\sqrt{a^2+b^2}\ge0\)
\(\Leftrightarrow\sqrt{a^2+b^2}\le1\)
\(\Leftrightarrow a^2+b^2\le1\)