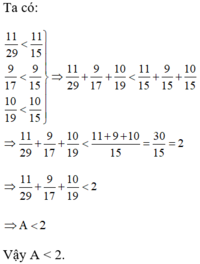không tính tổng, chứng tỏ rằng tổng A nhỏ hơn 2; A=15/27+9/17+108/21
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
0
VN
11
29 tháng 2 2016
Ta có:\(\frac{11}{29}\)<1
\(\frac{9}{17}\)<1 và\(\frac{10}{19}\)<1
=>A=\(\frac{11}{29}+\frac{9}{17}+\frac{10}{19}\)<1
=>A<2
23 tháng 2 2017
\(A=\frac{11}{29}+\frac{9}{17}+\frac{9}{19}+\frac{1}{19}\)
Tất cả ps đều nhỏ hơn 1/2
=> A<2
ung ho nhe
DH
23 tháng 2 2017
vi \(\frac{11}{29}\)<\(\frac{11}{15}\);\(\frac{9}{17}\)<\(\frac{9}{15}\);\(\frac{10}{19}\)<\(\frac{10}{15}\)
suy ra\(\frac{11}{29}+\frac{9}{17}+\frac{10}{19}< \frac{11}{15}+\frac{9}{15}+\frac{10}{15}\)
hay A<\(\frac{30}{15}\)hay A<2
DH
3
NN
26 tháng 3 2019
Gọi 2 số nghịch đảo nhau là a/b và b/a (a,b > 0)
Theo đề bài ta cần chứng minh a/b +b/a lớn hơn hoặc bằng 2
Không mất tính tổng quát, giả sử a lớn hơn hoặc bằng b, suy ra a = b + m (m lớn hơn hoặc bằng 0)
Ta có: a/b + b/a = (b+m)/b + b/(b+m) = 1 + m/b + b/(b+m)
\(\frac{a}{b}+\frac{b}{a}=\frac{b+m}{b}+\frac{b}{b+m}=1+\frac{m}{b}+\frac{b}{b+m}\)
NN
26 tháng 3 2019
\(\ge1+\frac{m}{b+m}+\frac{b}{b+m}=1+\frac{m+b}{b+m}=1+1=2\)
Vậy a/b + b/a lớn hơn hoặc bằng 2 (điều phải chứng minh)
NX
0