toán thi lớp chọn cấp 2 help
x/6+1/2=3/4+0,25
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 4 2023
Số học sinh giỏi toán so với số học sinh giỏi cấp trường chiếm
\(\dfrac{1}{3}\) ( số học sinh giỏi cấp trường)
Số học sinh giỏi ngoại ngữ so với số học sinh giỏi cấp trường chiếm:
\(\dfrac{1}{3}\) : \(\dfrac{4}{5}\) = \(\dfrac{5}{12}\) ( số học sinh giỏi cấp trường)
Phân số chỉ 6 học sinh giỏi văn là:
1 - \(\dfrac{1}{3}\) - \(\dfrac{5}{12}\) = \(\dfrac{1}{4}\)( số học sinh giỏi cấp trường)
Số học sinh giỏi cấp trường là
6 : \(\dfrac{1}{4}\) = 24 ( học sinh)
số học sinh giỏi toán là: 24 \(\times\) \(\dfrac{1}{3}\) = 8 ( học sinh)
Số học sinh giỏi ngoại ngữ là: 24 \(\times\) \(\dfrac{5}{12}\) = 10 ( học sinh)
Kết luận
Cách hai :
Gọi số học sinh giỏi cấp trường là \(x\) (học sinh, \(x\in\) N*)
Số học sinh giỏi toán là: \(x\times\) \(\dfrac{1}{3}\) = \(\dfrac{1}{3}\)\(x\)
Số học sinh giỏi ngoại ngữ là: \(\dfrac{1}{3}x:\dfrac{4}{5}\) = \(\dfrac{5}{12}\)\(x\)
Theo bài ra ta có:
\(x\) - \(\dfrac{1}{3}x-\dfrac{5}{12}x\) = 6
\(x\) \(\times\)( 1 - \(\dfrac{1}{3}-\dfrac{5}{12}\)) = 6
\(x\) \(\times\) \(\dfrac{1}{4}\) = 6
\(x\) = 6 \(\times\) 4 = 24
Số học sinh giỏi cấp trường là 24 học sinh
Số học sinh giỏi toán là: 24 \(\times\) \(\dfrac{1}{3}\) = 8 ( học sinh)
Số học sinh giỏi Ngoại ngữ là 24 \(\times\) \(\dfrac{5}{12}\) = 10 ( học sinh)
Kết luận: Số học sinh giỏi cấp trường là: 8 học sinh
Số học sinh giỏi toán là: 8 học sinh
Số học sinh giỏi ngoại ngữ là 10 học sinh
Số học sinh giỏi văn là 6 học sinh
CM
25 tháng 8 2019
Nhận xét: Số trung bình cộng điểm thi Toán của lớp 10A cao hơn lớp 10B nên có thể nói lớp 10A có kết quả thi môn Toán tốt hơn lớp 10B.
NH
4
19 tháng 4 2016
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HUYỆN HOẰNG HOÁ | ĐỀ THI HỌC SINH GIỎI LỚP 6 |
Bài 1 (4,5 điểm) Tính giá trị các biểu thức sau:
Bài 2 (4,0 điểm)
a. Tìm số tự nhiên x biết 8.6 + 288 : (x - 3)2 = 50
b. Tìm các chữ số x; y để chia cho 2; 5 và 9 đều dư 1.
c. Chứng tỏ rằng nếu p là số nguyên tố lớn hơn 3 thì p2 - 1 chia hết cho 3.
Bài 3 (4,5 điểm)
a. Cho biểu thức:
Tìm tất cả các giá trị nguyên của n để B là số nguyên.
b.Tìm các số nguyên tố x, y sao cho: x2 + 117 = y2
c. Số 2100 viết trong hệ thập phân có bao nhiêu chữ số .
Bài 4 (5,0 điểm)
Cho góc xBy = 550. Trên các tia Bx; By lần lượt lấy các điểm A; C (A ≠ B; C ≠ B). Trên đoạn thẳng AC lấy điểm D sao cho góc ABD = 300
a. Tính độ dài AC, biết AD = 4cm, CD = 3cm.
b. Tính số đo của góc DBC.
c. Từ B vẽ tia Bz sao cho góc DBz = 900. Tính số đo góc ABz.
Bài 5 (2,0 điểm)
a. Tìm các chữ số a, b, c khác 0 thỏa mãn:
b. Cho . Chứng minh A là số tự nhiên chia hết cho 5.
Đáp án đề thi học sinh giỏi môn Toán lớp 6
Bài 1 (4,5 điểm)
Bài 2 (4,0 điểm)
a. Biến đổi được: (x - 3)2 = 144 = 122 = (-12)2 ↔ x - 3 = 12 hoặc x - 3 = -12 ↔ x = 15 hoặc x = -9
Vì x là số tự nhiên nên x = -9 (loại). Vậy x = 15
b. Do chia cho 2 và 5 đều dư 1 nên y = 1. Ta có A =
Vì A = chia cho 9 dư 1 → - 1 chia hết cho 9 →
↔ x + 1 + 8 + 3 + 0 chia hết cho 9 ↔ x + 3 chia hết cho 9, mà x là chữ số nên x = 6
Vậy x = 6; y = 1
c. Xét số nguyên tố p khi chia cho 3.Ta có: p = 3k + 1 hoặc p = 3k + 2 (k ∈ N*)
Nếu p = 3k + 1 thì p2 - 1 = (3k + 1)2 -1 = 9k2 + 6k chia hết cho 3
Nếu p = 3k + 2 thì p2 - 1 = (3k + 2)2 - 1 = 9k2 + 12k chia hết cho 3
Vậy p2 - 1 chia hết cho 3.
Bài 3 (4,5 điểm)
a. Để B nhận giá trị nguyên thì n - 3 phải là ước của 5
=> n - 3 ∈ {-1; 1; -5; 5} => n ∈ { -2 ; 2; 4; 8}
Đối chiếu đ/k ta được n ∈ {- 2; 2; 4; 8}
b. Với x = 2, ta có: 22 + 117 = y2 → y2 = 121 → y = 11 (là số nguyên tố)
* Với x > 2, mà x là số nguyên tố nên x lẻ y2 = x2 + 117 là số chẵn
=> y là số chẵn
kết hợp với y là số nguyên tố nên y = 2 (loại)
Vậy x = 2; y = 11.
c. Ta có: 1030= 100010 và 2100 =102410. Suy ra: 1030 < 2100 (1)
Lại có: 2100= 231.263.26 = 231.5127.64 và 1031=231.528.53=231.6257.125
Nên: 2100< 1031 (2). Từ (1) và(2) suy ra số 2100 viết trong hệ thập phân có 31 chữ số.
CM
6 tháng 12 2017
Đáp án B
Phương pháp : Chia hai trường hợp :
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi.
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi.
Cách giải : Ω = C 2 n 3
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi. Có C n 2 . C n 1 cách
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi. Có C n 3 cách
Gọi A là biến cố học sinh TWO không phải thi lại
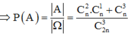
Đến đây chọn một giá trị bất kì của n rồi thay vào là nhanh nhất, chọn n =10 , ta tính được P ( A ) = 1 2
\(\frac{x}{6}+\frac{1}{2}=\frac{3}{4}+0,25\)
= \(\frac{2x}{12}+\frac{6}{12}=\frac{9}{12}+\frac{3}{12}\)
=> 2x + 6 =9 + 3
= 2x + 6 = 12
2x = 6
x = 3
Tìm x
\(\frac{x}{6}+\frac{1}{2}=\frac{3}{4}+0,25\)
\(\frac{x}{6}+\frac{1}{2}=\frac{3}{4}+\frac{1}{4}\)
\(\frac{x}{6}+\frac{1}{2}=1\)
\(\frac{x}{6}=1-\frac{1}{2}\)
\(\frac{x}{6}=\frac{2}{2}-\frac{1}{2}\)
\(\frac{x}{6}=\frac{1}{2}\)
\(\frac{x}{6}=\frac{3}{6}\)
\(x=3\)