Tính nhanh : 512 ; 3012; 992
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VK
3
5 tháng 8 2016
Đặt tổng trên = A
\(A=\frac{3}{2}+\frac{3}{8}+\frac{3}{32}+\frac{3}{128}+\frac{3}{512}\)
\(A.4=6+\frac{3}{2}+\frac{3}{8}+\frac{3}{32}+\frac{3}{128}\)
\(A.4-A=\left(6+\frac{3}{2}+\frac{3}{8}+\frac{3}{32}+\frac{3}{128}\right)-\left(\frac{3}{2}+\frac{3}{8}+\frac{3}{32}+\frac{3}{128}+\frac{3}{512}\right)\)
\(A.3=6-\frac{3}{512}=\frac{3069}{512}\)
\(A=\frac{3069}{512}:3=\frac{1023}{512}\)
5 tháng 8 2016
Đặt A = 3/2 + 3/8 + ... + 3/512
bn tách
3/2 = 3/2^1
3/8 = 3/2^3
...
3/512 = 3/2^9
Rồi nhân nó lên trừ được bao nhiêu - đi A ban đầu là đc
k nka
18 tháng 2 2016
512.(2 - 128) - 128.(-512) = 512.(2 - 128) - (-128).512 = 512.[2 - 128 - (-128)] = 512.2 = 1024
NC
6
20 tháng 8 2016
a, S = 1/2 + 1/4 + 1/8 +........+ 1/512
= \(\frac{1}{1.2}+\frac{1}{2.2}+\frac{1}{2.4}+...+\frac{1}{4.128}\)
\(\Rightarrow S=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+...+\frac{1}{4}-\frac{1}{128}\)
\(S=1-\frac{1}{128}=\frac{127}{128}\)
20 tháng 8 2016
S = 1/2 + 1/4 + 1/8 + ... + 1/512
2S = 2 x ( 1/2 + 1/4 + 1/8 + ... + 1/512 )
2S = 1 + 1/2 + 1/4 + ... + 1/256
2S - S = ( 1 + 1/2 + 1/4 + ... + 1/256 ) - ( 1/2 + 1/4 + 1/8 + ... + 1/512 )
S = 1 - 1/512
S = 511/512
PQ
0
P
0
NG
1
13 tháng 9 2015
a, 23 + 52 = 75
b, (-13) - 317 = -330
c, |-23| + 15 = 23 + 15 = 38
d, (-512) - 7 = -519
13 tháng 9 2015
23 + 52 = 75
(-13) + (-317) = -330
|-23| + 15 = 23 + 15 = 38
(-512) + (-7) = -519
PT
1
PT
1
CM
14 tháng 1 2019
− 5 12 + 6 11 + 7 17 + 5 11 + 5 12 = − 5 12 + 5 12 + 6 11 + 5 11 + 7 17 = 0 + 1 + 7 17 = 24 17
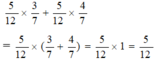
mng bỏ 992 đi nhé
Trả lời:
\(51^2=\left(50+1\right)^2\)
\(=50^2+2\times50\times1+1^2\)
\(=2500+100+1\)
\(=2601\)
\(301^2=\left(300+1\right)^2\)
\(=300^2+2\times300\times1+1^2\)
\(=90000+600+1\)
\(=90601\)
\(99^2=\left(100-1\right)^2\)
\(=100^2-2\times100+1\)
\(=10000-200+1\)
\(=9801\)
Học tốt