Cho tam giác ABC vuông tại A. Đường tròn nội tiếp tam giác ABC tiếp xúc với BC tại D
Chứng minh rằng SABC = BD . DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 8 2017
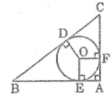
Gọi E và F lần lượt là tiếp điểm của đường tròn với AD và AC
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AE = AF
BE = BD
CD = CF
BD = BC + CD
BE = AB – AE
Suy ra: BD + BE = AB + BC – (AE + CD)
= AB + BC – (AE + CE)
= AB + BC – AC
Suy ra: BD = (AB + BC - AC)/2
Lại có: CD = BC – BD
CF = AC = AF
Suy ra: CD + CF = BC + AC – (BD + AF)
= BC + AC – (BE + AE)
= BC + AC – BA
Vậy S A B C = BD.DC.
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 1 2022
Pitago: \(BC^2=AB^2+AC^2\Rightarrow BC^2-\left(AB^2+AC^2\right)=0\)
Gọi các tiếp điểm với AB và AC là E và F
Do đường tròn (I) nội tiếp tam giác, theo t/c hai tiếp tuyến cắt nhau:
\(BD=BE\) ; \(AE=AF\) ; \(CD=CF\)
Mà \(BD+CD=BC;AE+BE=AB;AF+CF=AC\)
\(\Rightarrow BC+AB-AC=BD+CD+AB+BE-AF-CF=BD+BE=2BD\)
\(\Rightarrow BD=\dfrac{BC+AB-AC}{2}\)
Tương tự: \(BC+AC-AB=2DC\Rightarrow DC=\dfrac{BC+AC-AB}{2}\)
\(\Rightarrow BD.DC=\dfrac{1}{4}\left(BC+AB-AC\right)\left(BC+AC-AB\right)=\dfrac{1}{4}\left[BC^2-\left(AB-AC\right)^2\right]\)
\(=\dfrac{1}{4}\left(BC^2-\left(AB^2+AC^2\right)+2AB.AC\right)=\dfrac{1}{2}AB.AC=S_{ABC}\)
14 tháng 1 2019
a) +) Ta có: IB, IK là 2 tiếp tuyến kẻ từ I
=> IO là tia phân giác \(\widehat{BIK}\)=->\(\widehat{BIO}=\frac{1}{2}\widehat{KIB}\)(1)
Tương tự: \(\widehat{IBO}=\frac{1}{2}\widehat{IBC}\)(2)
+) ND cùng vuông góc với IK và BC
=> IK//BC
=> \(\widehat{KIB}+\widehat{IBC}=180^o\)(3)
Từ (1), (2), (3)
=> \(\widehat{IBO}+\widehat{BIO}=90^o\)=> \(\widehat{IBO}=90^o\)
+) Xét 2 tam giác vuông INO và ODB có:
\(\widehat{ION}=\widehat{OBD}\)( cùng phụ với góc BOD)
=> \(\Delta INO~\Delta ODB\)
=> \(\frac{IN}{OD}=\frac{ON}{BD}\)=> \(IN.BD=R^2\)( với R là bán kính đường tròn (O)) (4)
Tương tự ta cũng chứng minh được: \(NK.DC=R^2\)(5)
(4), (5)=> \(IN.BD=NK.DC\Rightarrow\frac{IN}{NK}=\frac{DC}{BD}\)(6)
b) IK//BC. Theo định lí Thaslet ta có:
\(\frac{IN}{BE}=\frac{NK}{EC}\left(=\frac{AN}{AE}\right)\Rightarrow\frac{IN}{NK}=\frac{BE}{EC}\)(7)
(6),(7)=> \(\frac{DC}{DB}=\frac{BE}{EC}\Rightarrow\frac{BC-BD}{DB}=\frac{BC-EC}{CE}\Rightarrow\frac{BC}{BD}-1=\frac{BC}{CE}-1\Rightarrow\frac{BC}{BD}=\frac{BC}{CE}\Rightarrow BD=CE\)
Q
13 tháng 11 2016
Gọi E, F lần lượt là tiếp điểm của đường tròn đã cho với các cạnh AB, AC. Đặt AE = AF = x. Ta có BD = BE, CF = CD. Từ đó ta có:
AB.AC = ( x + BD )( x + CD ) = x2 + ( BD + DC )x + BD.CD (1)
Do ABC là tam giác vuông nên theo định lý Pytago, ta có:
AB2 + AC2 = BC2 trở thành ( x + BD )2 + ( x + CD )2 = ( DB + DC )2 <=> ( x2 + ( BD + DC )x) = BD.DC <=> ( x + BD )( x + CD ) = 2BD.CD (2).
Từ (1), (2) suy ra đpcm.
HD
25 tháng 1 2017
cho 1 hinh duoc tao bang nua hinh tron co duong tron 2 dm va 1 hinh tam giac co duong cao 3dm,day2dm
lam on hay giup minh nhe! co giao minh sap kiem tra rui. cam on
CM
17 tháng 10 2017
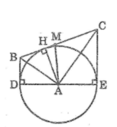
Gọi M là trung điểm của BC
Theo tính chất của tiếp tuyến, ta có:
AD ⊥ DB; AE ⊥ CE
Suy ra: BD // CE
Vậy tứ giác BDEC là hình thang
Khi đó MA là đường trung bình của hình thang BDEC
Suy ra: MA // BD ⇒ MA ⊥ DE
Trong tam giác vuông ABC ta có : MA = MB = MC
Suy ra M là tâm đường tròn đường kính BC với MA là bán kính
Vậy DE là tiếp tuyến của đường tròn tâm M đường kính BC.
Đặt BC = a , AC = b , AB = c . Ta có :
\(BD=\frac{a+c-d}{2}\)
\(DC=\frac{a+b-c}{2}\)
Do đó , ta giả sử \(\left(b\ge c\right)\)
\(BD.DC=\frac{a+c-b}{2}.\frac{a+b-c}{2}\)
\(=\frac{a-\left(b-c\right)}{2}.\frac{a+\left(b-c\right)}{2}\)
\(=\frac{a^2-\left(b-c\right)^2}{4}\)
\(=\frac{a^2-b^2+2bc-c^2}{4}\)
\(=\frac{a^2-\left(b^2+c^2\right)+2bc}{4}\)
Do \(a^2=b^2+c^2\)nên \(BD.DC=\frac{2bc}{3}=\frac{bc}{2}=S_{ABC}\)