CHO TAM GIÁC ABC CÓ BC DÀI 4,5CM.ĐIỂM I TRÊN AC SAO CHO AI =1/2 AC.HỔI ĐIỂM H CÁCH B MỘT ĐOẠN THẲNG BẰNG BAO NHIÊU ĐỂ IH CHIA TAM GIÁC ABC BẰNG 2 PHẦN MÀ DIỆN TÍCH PHẦN NÀY GẤP ĐÔI PHẦN KIA?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 6 2021
a/ . Gọi S là diện tích:
Ta có:
SBAHE = 2 SCEH
Vì BE = EC và hai tam giác BHE, HEC có cùng chiều cao hạ từ đỉnh chung H nên S(BHE) = S(HEC)
Do đó S(BAH)= S(BHE) = S(HEC)
Suy ra: S(ABC) = 3 S(BHA) và AC = 3 HA ( vì hai tam giác ABC và BHA có cùng chiều cao hạ từ đỉnh chung B)
Vậy HA = AC : 3 = 6 : 3 = 2 ( cm)
Nghĩa là điểm H phải tìm cách A là 2cm
b/ Ta có: S(ABC) = 6 x 3 : 2 = 9 ( cm2)
Vì BE = EC và hai tam giác BAE, EAC có cùng chiều cao hạ từ đỉnh chung A, nên S(BAE) = S(EAC) do đó:
S(EAC) = 0,5 S(ABC) = 9 : 2 = 4,5 (cm2)
Vì S(HEC) = 1/3 S(ABC) = 9 : 3 = 3 (cm2)
Nên S(AHE)= 4,5 – 3 = 1,5 (cm2)
TP
22 tháng 6 2021
a)
Ta có: SBAHE = 2 SCEH
Và SBHE = SHEC (BE=EC, chung đường cao kẻ từ H).
Do đó SBAH= SBHE = SHEC (1)
Suy ra SABC = 3SBHA. Mà hai tam giác ABC và BHA có chung đường cao kẻ từ B.
Nên HA = AC/3 = 6 : 3 = 2 ( cm).
b)
Ta lại có: SABC = 6 x 3 : 2 = 9 ( cm2).
SEAC = 1/2SABC = 9 : 2 = 4,5 (cm2) (EC = ½ BC, chung đường cao kẻ từ A).
Từ (1) cho ta: SEHC = 9 : 3 = 3 (cm2)
Mà: SAEH = SAEC – SEHC = 4,5 – 3 = 1,5 (cm2)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 6 2023
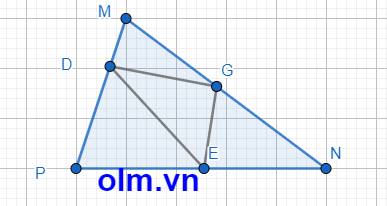
Tỉ số diện tích tam giác PDE và diện tích tứ giác DMNE là:
1 : 2 = \(\dfrac{1}{2}\)
Ta có sơ đồ: 
Theo sơ đồ ta có: Diện tích tam giác BDE = 360 : (1+2) = 120 (cm2)
Diện tích tứ giác DMNE là: 360 - 120 = 240 (cm2)
SMEP = \(\dfrac{1}{2}\)SMNP vì ( hai tam giác có chung đường cao hạ từ đỉnh M xuống đáy PN và PE = \(\dfrac{1}{2}\) PN)
SMEP = 360 \(\times\) \(\dfrac{1}{2}\) = 180(cm2)
Tỉ số diện tích SDEP và SMEP là: 120 : 180 = \(\dfrac{2}{3}\) ⇒ PD = \(\dfrac{2}{3}\) PM ( vì hai tam giác có chung đường cao hạ từ đỉnh E xuống đáy PM nên tỉ số diện tích hai tam giác là tỉ số của hai cạnh đáy)
Cạnh MD bằng: 1 - \(\dfrac{2}{3}\) = \(\dfrac{1}{3}\) (cạnh PM)
SMGD = \(\dfrac{1}{3}\) SMGP ( Vì hai tam giác có chung đường cao hạ từ đỉnh G xuống đáy PM và MD = \(\dfrac{1}{3}\) PM)
SMGP = \(\dfrac{1}{2}\) SMNP ( Vì hai tam giác có chung đường cao hạ từ đỉnh P xuống đáy MN và MG = \(\dfrac{1}{2}\) MN)
⇒ SMGP = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{2}\) SMNP = \(\dfrac{1}{3}\) \(\times\) \(\dfrac{1}{2}\) \(\times\) 360 = 60 (cm2)
SGEN = \(\dfrac{1}{2}\)SGPN ( vì hai tam giác có chung đường cao hạ từ đỉnh G xuông đáy PN và EN = \(\dfrac{1}{2}\)PN)
Tương tự ta có: SGPN = \(\dfrac{1}{2}\) SMNP
⇒ SGEN = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{1}{2}\) \(\times\) 360 = 90 (cm2)
SGDE = SMNED - SMGD - SGEN = 240 - 60 -90 = 90 (cm2)
Đáp số: 90 cm2
1. Xét hai tam giác vuông ΔABHΔABH và ΔACHΔACH có:
AHAH cạnh chung
AB=AC=10cmAB=AC=10cm (gt)
Vậy ΔABH=ΔACHΔABH=ΔACH (cạnh huyền- cạnh góc vuông)
HC=HBHC=HB (hai cạnh tương ứng) hay H là trung điểm BC
2. BH=HC=BC2=122=6BH=HC=BC2=122=6 cm
Áp dụng định lí Py-ta-go vào ΔΔ vuông ABHABH có:
AH2=AB2−HB2=102−62=64⇒AH=8AH2=AB2−HB2=102−62=64⇒AH=8 cm
3. Xét ΔAKEΔAKE và ΔAKHΔAKH có:
AKAK chung
ˆAKE=ˆAKH=90oAKE^=AKH^=90o (do HK⊥ACHK⊥AC)
KE=KHKE=KH (do giả thiết cho K là trung điểm của HE)
⇒ΔAKE=ΔAKH⇒ΔAKE=ΔAKH (c.g.c)
⇒AE=AH⇒AE=AH (hai cạnh tương ứng) (1)
Cách khác để chứng minh AE=AH
Do ΔAHEΔAHE có K là trung điểm của HE nên AK là đường trung tuyến,
Có HK⊥ACHK⊥AC hay AK⊥HEAK⊥HE nên AK là đường cao
ΔAHEΔAHE có AK là đường trung tuyến cũng là đường cao nên ΔAHEΔAHE cân đỉnh A nên AE=AH.
4. Ta có HI⊥ABHI⊥AB hay AI⊥DH⇒AI⊥DH⇒ AI là đường cao của ΔADHΔADH
Mà IH=ID nên AI cũng là đường trung tuyến ΔADHΔADH
Vậy ΔAEHΔAEH cân tại A
Nên AD=AH (2)
Từ (1) và (2) suy ra AE=AD hay ΔAEDΔAED cân tại A.
5. Xét 2 tam giác vuông ΔAHIΔAHI và ΔAHKΔAHK có:
AH chung
ˆIAH=ˆKAHIAH^=KAH^ (hai góc tương ứng của ΔABH=ΔACHΔABH=ΔACH)
⇒ΔAHI=ΔAHK⇒ΔAHI=ΔAHK (cạnh huyền- góc nhọn)
⇒HI=HK⇒2HI=2HK⇒HD=HE⇒HI=HK⇒2HI=2HK⇒HD=HE
Mà ta có AD=AEAD=AE (cmt)
⇒AH⇒AH là đường trung trực của DE⇒AH⊥DEDE⇒AH⊥DE mà AH⊥BCAH⊥BC
⇒DE//BC⇒DE//BC
6. Để A là trung điểm ED thì DA⊥AHDA⊥AH mà ΔADHΔADH cân (cmt) nên ΔADHΔADH vuông cân đỉnh A.
Có AIAI là đường cao, đường trung tuyến nên AIAI cũng là đường phân giác nên
ˆDAI=ˆHAI=90o2=45oDAI^=HAI^=90o2=45o
⇒ˆIAH=ˆBAH=ˆCAH=45o⇒IAH^=BAH^=CAH^=45o (do ΔABH=ΔACHΔABH=ΔACH)
⇒ˆBAC=ˆBAH+ˆCAH=90o⇒BAC^=BAH^+CAH^=90o và ΔABCΔABC cân đỉnh A
⇒ΔABC⇒ΔABC vuông cân đỉnh A.
Vậy nếu ΔABCΔABC vuông cân đỉnh A thì AA là trung điểm của DE.