Với giá trị nào của m thì pt \(\left(3cosx-2\right)\left(2cosx+3m-1\right)=0\) có đúng 3 nghiệm phân biệt thuộc khoảng \(\left(0;\frac{3\pi}{2}\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
16 tháng 2 2021
a, Phương trình có hai nghiệm trái dấu khi \(2\left(2m^2-3m-5\right)< 0\)
\(\Leftrightarrow\left(2m-5\right)\left(m+1\right)< 0\)
\(\Leftrightarrow-1< m< \dfrac{5}{2}\)
b, TH1: \(m^2-3m+2=0\Leftrightarrow\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\)
Phương trình đã cho có nghiệm duy nhất
TH2: \(m^2-3m+2\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m\ne2\end{matrix}\right.\)
Phương trình có hai nghiệm trái dấu khi \(-5\left(m^2-3m+2\right)< 0\)
\(\Leftrightarrow m^2-3m+2>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>2\\m< 1\end{matrix}\right.\)
Vậy \(m>2\) hoặc \(m< 1\)
HP
1 tháng 8 2021
1.
\(cos2x-3cosx+2=0\)
\(\Leftrightarrow2cos^2x-3cosx+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(x=k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow\) không có nghiệm x thuộc đoạn
\(x=\pm\dfrac{\pi}{3}+k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow x_1=\dfrac{\pi}{3};x_2=\dfrac{5\pi}{3}\)
\(\Rightarrow P=x_1.x_2=\dfrac{5\pi^2}{9}\)
HP
1 tháng 8 2021
2.
\(pt\Leftrightarrow\left(cos3x-m+2\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\left(1\right)\\cos3x=m-2\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\)
Ta có: \(x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\pm\dfrac{\pi}{9}\)
Yêu cầu bài toán thỏa mãn khi \(\left(2\right)\) có nghiệm duy nhất thuộc \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\m-2=1\\m-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=3\\m=1\end{matrix}\right.\)
TH1: \(m=2\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\dfrac{\pi}{6}\left(tm\right)\)
\(\Rightarrow m=2\) thỏa mãn yêu cầu bài toán
TH2: \(m=3\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=0\left(tm\right)\)
\(\Rightarrow m=3\) thỏa mãn yêu cầu bài toán
TH3: \(m=1\)
\(\left(2\right)\Leftrightarrow cos3x=-1\Leftrightarrow x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{1}{3}\\x=-1\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow m=2\) không thỏa mãn yêu cầu bài toán
Vậy \(m=2;m=3\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2021
Với \(m=2\Rightarrow6x^2+3=0\) (vô nghiệm)
Với \(m\ne2\) đặt \(x^2=t\ge0\Rightarrow\left(m-2\right)t^2-2\left(m+1\right)t-3=0\) (1)
Ứng với mỗi \(t>0\Rightarrow\) luôn có 2 giá trị x phân biệt tương ứng thỏa mãn
\(\Rightarrow\) Pt đã cho có đúng 2 nghiệm pb khi và chỉ khi (1) có 2 nghiệm trái dấu
\(\Leftrightarrow ac< 0\Leftrightarrow-3\left(m-2\right)< 0\Leftrightarrow m>2\)
22 tháng 11 2015
\(\left(m+1\right)x^3+\left(3m-1\right)x^2-x-4m+1=0\)
<=> (m.x3 - m) + (x3 - x) + (3mx2 - 3m) - (x2 - 1) = 0
<=> m(x - 1)(x2 + x + 1) + x(x - 1).(x+1) + 3m(x - 1)(x+1) - (x -1)(x+ 1) = 0
<=> (x - 1).[m(x2 + x+ 1) + x(x+1) + 3m(x+ 1) - (x+1)] = 0
<=> (x - 1).(mx2 + mx + m + x2 + x + 3mx + 3m - x - 1) = 0
<=> (x - 1).[(m + 1)x2 + 4mx + 4m - 1)] = 0 (*)
b) (*) <=> x = 1 hoặc (m + 1)x2 + 4mx + 4m - 1) = 0 (1)
Để (*) có 3 nghiệm phân biệt trong đó có 2 ngiệm âm <=> (1) có 2 nghiệm âm phân biệt
<=> m+ 1 \(\ne\) 0 và \(\Delta\)' > 0 và x1.x2 > 0 và x1 + x2 < 0 trong đó x1; x2 là hai nghiệm của (1)
+) m + 1 \(\ne\) 0 <=> m \(\ne\) - 1
+) \(\Delta\)' = (2m)2 - (m + 1).(4m- 1) = 4m2 - 4m2 - 3m + 1 = -3m + 1 > 0 => m < 1/3
+) Theo hệ thức Vi ét ta có: x1 + x2 = \(-\frac{4m}{m+1}\); x1.x2 = \(\frac{4m-1}{m+1}\)
=> \(-\frac{4m}{m+1}\) < 0 và \(\frac{4m-1}{m+1}\) > 0
=> \(\frac{4m}{m+1}>0\) và \(\frac{4m+1}{m+1}\) > 0 => \(\frac{4m}{m+1}\) > 0 => 4m và m + 1 cùng dấu
=> m > 0 hoặc m < -1
Kết hợp điều kiện m < 1/3 và m \(\ne\) -1 => m < - 1 hoặc 0 < m < 1/3
Vậy...
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2021
Đặt \(x^2=t\ge0\Rightarrow f\left(t\right)=t^2-\left(2m+1\right)t+m+3=0\) (1)
Pt đã cho có 4 nghiệm pb khi (1) có 2 nghiệm pb đều dương
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(2m+1\right)^2-4\left(m+3\right)>0\\t_1+t_2=2m+1>0\\t_1t_2=m+3>0\end{matrix}\right.\) \(\Rightarrow m>\dfrac{\sqrt{11}}{2}\)
Không mất tính tổng quát, giả sử 2 nghiệm dương của (1) là \(t_1< t_2\)
Khi đó 4 nghiệm của pt đã cho là: \(-\sqrt{t_2}< -\sqrt{t_1}< \sqrt{t_1}< \sqrt{t_2}\)
Do đó điều kiện đề bài tương đương:
\(\left\{{}\begin{matrix}-\sqrt{t_2}< -2\\-\sqrt{t_1}>-1\\\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}t_2>4\\t_1< 1\end{matrix}\right.\)
Bài toàn trở thành: tìm m để (1) có 2 nghiệm dương pb thỏa mãn: \(t_1< 1< 4< t_2\)
\(\Rightarrow\left\{{}\begin{matrix}1.f\left(1\right)< 0\\1.f\left(4\right)< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}1-\left(2m+1\right)+m+3< 0\\16-4\left(2m+1\right)+m+3< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>3\\m>\dfrac{15}{7}\end{matrix}\right.\) \(\Rightarrow m>3\)
Kết hợp \(m>\dfrac{\sqrt{11}}{2}\Rightarrow m>3\)
30 tháng 4 2022
Để pt 1 có 2 nghiệm phân biệt =>\(\Delta\)>0
<=> (2m-1(2 - 4(m2-3m-4( >0
<=> 4m2 - 4m + 1 - 4m2+12m+16 > 0
<=>8m +17>0
<=> m>-17/8
=> theo hệ thức Vi ét ta có
x1+x2=-2m+1 *
x1.x2=m2-3m-4 *
Theo bài ra ta có pt
|x1−x2|−2=0
<=> |x1−x2|=2
<=> (x1-x2(2=22
<=> x12 - 2x1.x2 + x22 = 4
<=> (x1 + x2 > 2- 4 x1x2 = 4 <**>
Thay *,* vào <**> ta được :
(-<2m-1>>2 - 4<m2-3m-4> = 4
<=> 4m2-4m+1 - 4m2+12m+16=4
<=> 8m + 17= 4
<=> 8m = 13
<=> m= 13/8 < t/m >
Vậy m = 13/8 là giá trị cần tìm
AH
Akai Haruma
Giáo viên
30 tháng 4 2022
Lời giải:
Để pt có 2 nghiệm pb thì:
$\Delta'=(2m-1)^2-4(m^2-3m-4)=8m+17>0\Leftrightarrow m> \frac{-17}{8}$
Áp dụng định lý Viet:
$x_1+x_2=1-2m$
$x_1x_2=m^2-3m-4$
Khi đó:
$|x_1-x_2|-2=0$
$\Leftrightarrow |x_1-x_2|=2$
$\Leftrightarrow (x_1-x_2)^2=4$
$\Leftrightarrow (x_1+x_2)^2-4x_1x_2=4$
$\Leftrightarrow (1-2m)^2-4(m^2-3m-4)=4$
$\Leftrightarrow 8m+17=4$
$\Leftrightarrow m=\frac{-13}{8}$ (tm)
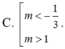
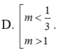
Sử dụng đường tròn lượng giác, ta thấy \(3cosx-2=0\) có đúng 1 nghiệm thuộc \(\left(0;\frac{3\pi}{2}\right)\)
Vậy để pt đã cho có 3 nghiệm pb thuộc \(\left(0;\frac{3\pi}{2}\right)\) thì \(2cosx+3m-1=0\) có 2 nghiệm pb sao cho \(-1< cosx< 0\)
\(2cosx+3m-1=0\Rightarrow cosx=\frac{1-3m}{2}\)
\(\Rightarrow-1< \frac{1-3m}{2}< 0\Rightarrow\left\{{}\begin{matrix}\frac{3-3m}{2}>0\\\frac{1-3m}{2}< 0\end{matrix}\right.\)
\(\Rightarrow\frac{1}{3}< m< 1\)