Mọi người cho e hỏi là tại sao hàm số đồng biến trên (a; +∞) thì hai nghiệm đều nhỏ hơn a ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: Để (d) là hàm số bậc nhất thì 2m-2<>0
hay m<>1
b: Để (d) là hàm số đồng biến thì 2m-2>0
hay m>1
c: Hàm số (d') đồng biến vì a=4>0
Bài 2:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-x+6=3x-6\\y=-x+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)

a) y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+) m2 + 5m = 0 ⇔ 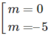
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
Δ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.
b) Nếu hàm số đạt cực đại tại x = 1 thì y’(1) = 0. Khi đó:
y′(1) = –3
m
2
– 3m + 6 = 0 ⇔ 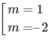
Mặt khác, y” = –6( m 2 + 5m)x + 12m
+) Với m = 1 thì y’’ = -36x + 12. Khi đó, y’’(1) = -24 < 0 , hàm số đạt cực đại tại x = 1.
+) Với m = -2 thì y’’ = 36x – 24. Khi đó, y’’(1) = 12 > 0, hàm số đạt cực tiểu tại x = 1.
Vậy với m = 1 thì hàm số đạt cực đại tại x = 1.

1:
a: m^2+1>=1>0 với mọi m
=>y=(m^2+1)x-5 luôn là hàm số bậc nhất
b: Do m^2+1>0 với mọi m
nên hàm số y=(m^2+1)x-5 đồng biến trên R

y = –( m 2 + 5m) x 3 + 6m x 2 + 6x – 5
y′ = –3( m 2 + 5m) x 2 + 12mx + 6
Hàm số đơn điệu trên R khi và chỉ khi y’ không đổi dấu.
Ta xét các trường hợp:
+)
m
2
+ 5m = 0 ⇔ 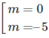
– Với m = 0 thì y’ = 6 nên hàm số luôn đồng biến.
– Với m = -5 thì y’ = -60x + 6 đổi dấu khi x đi qua .
+) Với m 2 + 5m ≠ 0. Khi đó, y’ không đổi dấu nếu
∆ ' = 36 m 2 + 18( m 2 + 5m) ≤ 0 ⇔ 3 m 2 + 5m ≤ 0 ⇔ –5/3 ≤ m ≤ 0
– Với điều kiện đó, ta có –3( m 2 + 5m) > 0 nên y’ > 0 và do đó hàm số đồng biến trên R.
Vậy với điều kiện –5/3 ≤ m ≤ 0 thì hàm số đồng biến trên R.

a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3

Hàm số y = (3 - 2 )x + 1 có hệ số a = 3 - 2 , hệ số b = 1
Ta có: a = 3 - 2 > 0 nên hàm số đồng biến trên R

Ai bảo bạn thế? Ví dụ hàm $f(x)=x^2+2x$ đồng biến trên $(-1;+\infty)$ nhưng nó có nghiệm $x=0$ lớn hơn $-1$ đấy.