Cho đường tròn tâm (O) và điểm K nằm ngoài đường tròn. Từ K kẻ các tiếp tuyến KA,KB đến (O). Một đường thẳng qua K cắt (O) tại C,D sao cho C nằm giữa K và D, đồng thời hai điểm O, A nằm khác phía so với CD.
a) CM tứ giác OAKB nội tiếp và KA2= KC.KD
b) Gọi M là giao điểm của đoạn OK và AB. CM góc KMC=KDO
c) Kẻ đường kính AI của (O). Gọi G, N lần lượt là giao điểm của OK với các đoạn CI, DI. Chứng...
Đọc tiếp
Cho đường tròn tâm (O) và điểm K nằm ngoài đường tròn. Từ K kẻ các tiếp tuyến KA,KB đến (O). Một đường thẳng qua K cắt (O) tại C,D sao cho C nằm giữa K và D, đồng thời hai điểm O, A nằm khác phía so với CD.
a) CM tứ giác OAKB nội tiếp và KA2= KC.KD
b) Gọi M là giao điểm của đoạn OK và AB. CM góc KMC=KDO
c) Kẻ đường kính AI của (O). Gọi G, N lần lượt là giao điểm của OK với các đoạn CI, DI. Chứng minh tứ giác AMND nội tiếp và OG=ON.
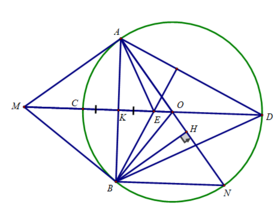
Cho đường tròn tâm (O) và điểm K nằm ngoài đường tròn. Từ K kẻ các tiếp tuyến KA,KB đến (O). Một đường thẳng qua K cắt (O) tại C,D sao cho C nằm giữa K và D, đồng thời hai điểm O, A nằm khác phía so với CD.
a) CM tứ giác OAKB nội tiếp và KA2= KC.KD
b) Gọi M là giao điểm của đoạn OK và AB. CM góc KMC=KDO
c) Kẻ đường kính AI của (O). Gọi G, N lần lượt là giao điểm của OK với các đoạn CI, DI. Chứng minh tứ giác AMND nội tiếp và OG=ON.
:))