Trên bờ của 1 cái ao hình tròn )O) có 3 cây dừa ở A, B, C là các đỉnh của 1 tam giác đều. Bác Tiến muốn trồng 1 cây cột điện trên bờ BC ( cung nhỏ BC của đường tròn tâm (O)) tại vị trí M sao cho MA+MB+MC đạt giá trị lớn nhất. Hỏi M phải đặt ở đau cho đúng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét \(\Delta MBD\)cân tại M có :
\(\widehat{BDM}=60^0\)
\(\Rightarrow\Delta MBD\)là tam giác đều
\(\Rightarrow\widehat{BDM}=60^0\)
\(\Rightarrow\widehat{BDA}=120^0\)
\(\Rightarrow\)Khi M di chuyển trên cung nhỏ BC thì M di chuyển trên cung tròn ( nằm trên nửa mặt phẳng bờ AB chưa điểm M ) nhìn AB một góc bằng \(120^0\)
Xét \(\Delta DBA\)và \(\Delta MBC\)có :
\(BA=BC\)( vì tam giác ABC đều )
\(\widehat{BAD}=\widehat{BCM}\)( cùng chắn cung BM )
\(\widehat{ABD}=\widehat{CBM}\left(=60^0-\widehat{DBC}\right)\)
Suy ra \(\Delta DBA=\Delta MBC\)
\(\Rightarrow MC=DA\)
\(\Rightarrow MA+MB+MC=MA+MD+DA=2MA\)
\(MA+MB+MC\)lớn nhất khi MA lớn nhất
\(\Rightarrow AM\)là đường kính của \(\left(O\right)\)
\(\Rightarrow M\)là điểm chính giữa của cung BC
Chúc bạn học tốt !!!

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề

Chọn B.
Phương pháp: Sử dụng phương pháp tọa độ trong mặt phẳng.
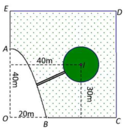
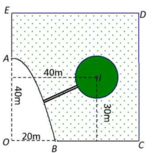
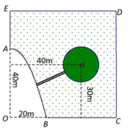
Cách giải: Chọn hệ trục tọa độ Đề các vuông góc như sau:
Gốc O, chiều dương trục hoành là tia OC, chiều dương trục tung là tia OE, đơn vị hai trục là đơn vị độ dài 1m
Khi đó ta có phương trình Parabol là

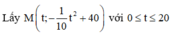
nằm trên Parabol thì khoảng cách ngắn nhất từ đường tròn đến M là
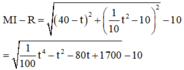
Khảo sát hàm số suy ra khoảng cách ngắn nhất xấp xỉ 17,7
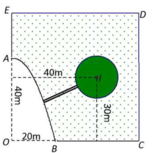

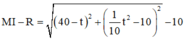
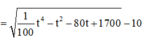
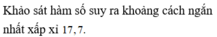
Gọi chiều cao của cây là h = AB và cọc tiêu DC = 2m.
Khoảng cách từ chân đến mắt người đo là FE = 1,6m.
Cọc xa cây một khoảng HG = 15m, và người cách cọc một khoảng CE= 0,8m và gọi I là giao điểm của BD và AC.
Ta có: AB ⊥ AI, DC ⊥ AI, FE ⊥ AI
⇒ AB // DC // FE.
Ta có: ΔEFI ΔCDI (vì EF // CD)
ΔCDI (vì EF // CD)
=> EFCDEFCD=EICIEICI
Mà CD = 2m , EF = 1,6m
Nên 1,621,62=EICIEICI=>EICIEICI=4545=>EI4EI4=CI5CI5
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
EI4EI4= CI5CI5=CI−EI5−4CI−EI5−4=CE1CE1=0,8
=>EI1EI1=0,8=> EI = 0,8.4 = 3,2
=>CI5CI5=0,8=> CI= 0,8.5 = 4
Mà CI – EI = CE = 0,8
⇒ EI = 0,8.4 = 3,2m; CI = 5.0,8 = 4m.
⇒ AI = AC + AE + EI = 15 + 0,8 + 3,2 = 19m
+ ΔCDI ΔABI (vì CD // AB)
ΔABI (vì CD // AB)
CIAICIAI=CDABCDAB
AB=CD.AICICD.AICI=2.1942.194=9,5 m
Vậy cây cao 9,5m.