Cho các số thực a;b;c > 1 . Chứng minh rằng 1/(2a - 1) + 1/(2b - 1) + 1/(2c - 1) + 4ab/(1 + ab) + 4bc/(1 + bc) + 4ca/(1 + ca) > 9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) \({x^2} = 4 = {2^2} = {\left( { - 2} \right)^2} \Leftrightarrow x = \pm 2\)
b) \({x^3} = - 8 = {\left( { - 2} \right)^3} \Leftrightarrow x = - 2.\)
- Chú ý:
Trong toán học, căn bậc chẵn của một số là một số lớn hơn 0. Do đó số âm không có căn bậc chẵn.

CM
7 tháng 5 2018
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:


CM
25 tháng 3 2019
Giả sử phương trình đã cho có 3 nghiệm
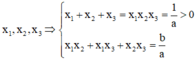
Khi đó
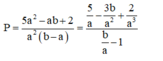
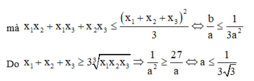
Suy ra
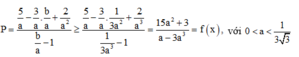
Xét hàm số:
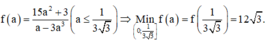
Chọn D.

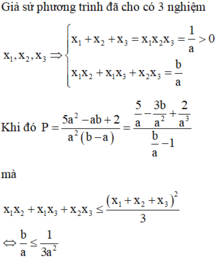
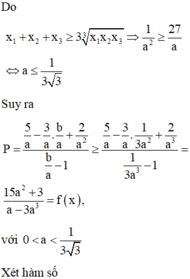
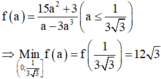
Do \(a,b,c\ge1\) nên \(\left(a-1\right)\left(b-1\right)\ge0\Leftrightarrow ab+1\ge a+b\)
Mà \(\frac{4ab}{1+ab}=\frac{4\left(1+ab\right)-4}{1+ab}=4-\frac{4}{1+ab}\ge4-\frac{4}{a+b}\)
Tương tự:\(\frac{4bc}{1+bc}\ge4-\frac{4}{b+c};\frac{4ca}{1+ca}\ge4-\frac{4}{c+a}\)
Mặt khác:\(\left(a-1\right)^2\ge0\Leftrightarrow a^2\ge2a-1\)
Tương tự:\(b^2\ge2b-1;c^2\ge2c-1\)
Khi đó ta có:
\(LHS\ge\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+12-4\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)=S\)
Áp dụng AM - GM ta dễ có:\(\frac{1}{a^2}+\frac{1}{b^2}\ge\frac{2}{ab}\ge\frac{2}{\frac{\left(a+b\right)^2}{4}}=\frac{8}{\left(a+b\right)^2}\)
\(\Rightarrow\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{4}{\left(a+b\right)^2}+\frac{4}{\left(b+c\right)^2}+\frac{4}{\left(c+a\right)^2}\)
\(\Rightarrow S\ge\frac{4}{\left(a+b\right)^2}+\frac{4}{\left(b+c\right)^2}+\frac{4}{\left(c+a\right)^2}+12-4\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\)
\(=\left(\frac{2}{a+b}-1\right)^2+\left(\frac{2}{b+c}-1\right)^2+\left(\frac{2}{c+a}-1\right)^2+9\)
\(\ge9\)
Vậy ta có đpcm
Đẳng thức xảy ra tại \(a=b=c=1\)
Mình cảm ơn bạn