Cho điểm M nằm trên đường trung trực của đoạn thẳng AB. Biết khoảng cách từ điểm M đến AB = 4cm và AB = 6cm. Tính MA, MB. Giúp mình với mình ko biết làm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 6 2022
Gọi giao của d và AB là C
=>C là trung điểm của AB và MC=4cm
=>CA=CB=AB/2=3cm
\(MA=MB=\sqrt{3^2+4^2}=5\left(cm\right)\)
27 tháng 6 2022
Gọi giao của d và AB là C
=>C là trung điểm của AB và MC=4cm
=>CA=CB=AB/2=3cm
\(MA=MB=\sqrt{3^2+4^2}=5\left(cm\right)\)
23 tháng 12 2018
Cậu tự vẽ hình nhé (theo tớ) !! Cho CD là trung trực của AB, O là giao điểm, kẻ 1 điểm M bất kì. Nối A với M, B với M
Bài làm
Xét tam giác AOM và BOM
Có AO = OB (GT)
Góc O1 = O2 ( CD là trung trực của AB)
OM cạnh chung
=> Tam giác AOM = BOM (c.g.c)
=> MA = MB ( 2 cạnh tương ứng )
>> Nhớ cho mik nhé ! ❤
CM
16 tháng 3 2019
Gọi trung điểm của AB là I
Ta có tam giác AMI vuông tại I. Theo định lý Pytago ta có
IM2 = AM2 - AI2 = 62 - 42 = 20 ⇒ IM = 20 c m . Chọn C
HT
8 tháng 7 2016
Gọi NM là trung trực AB
=> NA = NB và góc MNA = góc MNB = 90o (Tính chất đường trung trực)
Xét tam giác MNA và tam giác MNB có:
góc MNA = góc MNB (= 90o)
Chung NM
NA = NB (cmt)
=> tam giác MNA = tam giác MNB (c.g.c)
=> MA = MB (2 cạnh tương ứng)
PT
Cho đoạn thẳng AB, điểm M nằm trên đường trung trực của AB. So sánh độ dài các đoạn thẳng MA ,và MB.
1
CM
28 tháng 3 2017
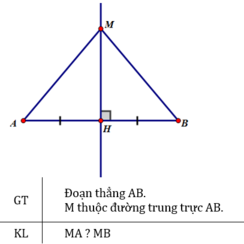
Gọi H là giao điểm của đường trung trực với đoạn AB
⇒ H là trung điểm AB và MH ⊥ AB.
Xét ΔAHM và ΔBHM có:
Nên ΔAHM = ΔBHM
Vậy MA = MB
Gọi giao điểm của 2 đoạn thẳng AB và đg trung trực là H
HA=HB=3 cm
Xét tam giác vuông AHM , ta có
AM2= AH2+MH2 ( định lý py-ta-go)
hay AM2= 32+42= 9 +16= 25
=> AM=\(\sqrt{25}\)=5 cm
mà MA=MB (gt)
=> MA=MB=5cm
Chúc bạn học tốt