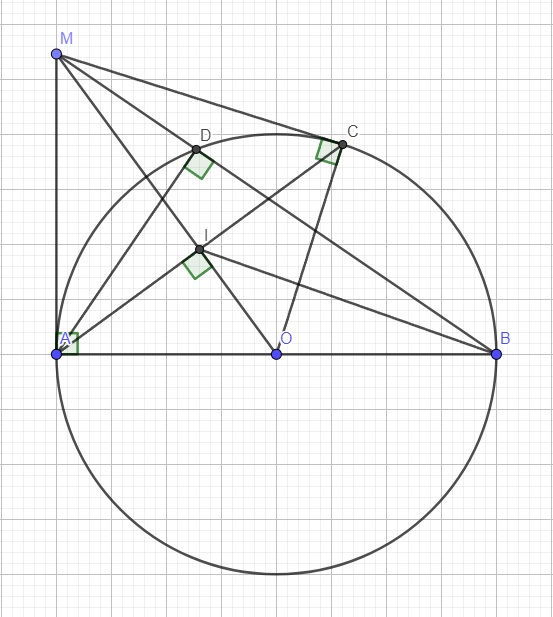
Cho đường tròn (O), đường kính AB. Trên tiếp tuyến của đường tròn (O) tại A lấy điểm M (M khác A). Từ M vẽ tiếp tuyến thứ hai MC với (O) (C là tiếp tuyến đường tròn (O) tại A lấy điểm M (M khác A). Từ M vẽ tiếp tuyến thứ hai là K và cắt CH tại N. Chứng minh rằng :
a) Tứ giác AKNH nội tiếp
b) \(MC^2=MK.MB\)
C) ∠ KAC = ∠ OMB