Cho hình thang ABCD có đáy bé bằng \(\frac{1}{3}\)đáy lớn và có diện tích bằng 24cm2. Kéo dài DA và CB cắt nhau tại M. Tính diện tích tam giác MAB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 2 2017
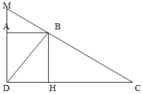
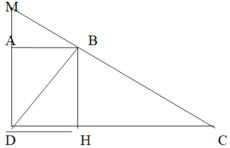
Nối B với D, kẽ đường cao BH ta có:
S B A D = S D B H vì ADBH là hình chữ nhật.
Mặt khác S D B H = 1 / 3 S D B C vì DH =1/3 DC
Nên S B A D = 1 / 4 S A B C D
= 24 : 4 = 6 ( c m 2 )
Và S D B C = 24 - 6 = 18 ( c m 2 )
Tam giác DBM và tam giác DCM có chung đáy MD và chiều cao BA = 1/3CD
Do đó : S B D M = 1 / 3 S C D M
Suy ra: S B D M = 1 / 2 S D B C
= 1/2 x 18 = 9 ( c m 2 )
Vì S M A B = S B D M - S B A D nên: S M A B = 9 - 6 = 3 ( c m 2 )
Đáp số : S M A B = 3 c m 2
27 tháng 4 2016
Mình học lớp 4 rồi nhưng bạn có thể vẽ hình được không?Con lười=)))Vừa mới thi học sinh giỏi về
CM
7 tháng 12 2019
S(ABD) = 1/3 S(ACD)
Mà hai hình này chung đáy AD => chiều cao hạ từ B = 1/3 chiều cao hạ từ C.
=> S(MAB) = 1/3 S(MAC)
=> S(MAB) = 1/2 S(ABC)
S(ABC) = 1/3 S(ACD) = 1/4 S(ABCD)
=> S(MAB) = 1/2 x 1/4 = 1/8 S(ABCD)
Vậy S(MAB) = 16 x 1/8 = 2 cm2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 5 2022
Hai tg ABC và tg ACD có đường cao từ C->AB = đường cao từ A->CD nên
\(\dfrac{S_{ABC}}{S_{ACD}}=\dfrac{AB}{CD}=\dfrac{1}{3}\Rightarrow S_{ACD}=3xS_{ABC}\)
\(\Rightarrow S_{ABCD}=S_{ABC}+S_{ACD}=S_{ABC}+3xS_{ABC}=4xS_{ABC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{4}xS_{ABCD}\)
Kéo dài AB, từ C dựng đường thẳng song song với AD cắt AB kéo dài tại E => AECD là hình chữ nhật
\(\Rightarrow AE=CD\Rightarrow AB=\dfrac{1}{3}CD=\dfrac{1}{3}AE\Rightarrow AB=\dfrac{1}{2}xBE\)
Hai tg ABC và tg EBC có chung đường cao từ C->AB nên
\(\dfrac{S_{ABC}}{S_{EBC}}=\dfrac{AB}{BE}=\dfrac{1}{2}\)
Hai tg này có chung BC nên
\(\dfrac{S_{ABC}}{S_{EBC}}=\) đường cao từ A->BC = đường cao từ E->BC\(=\dfrac{1}{2}\)
Hai tg AMC và tg EMC có chung MC nên
\(\dfrac{S_{AMC}}{S_{EMC}}=\)đường cao từ A->BC = đường cao từ E->BC\(=\dfrac{1}{2}\)
Hai tg AMC và tg AME có chung AM và đường cao từ C->AD = đường cao từ E->AD nên
\(S_{AMC}=S_{AME}\Rightarrow\dfrac{S_{AME}}{S_{EMC}}=\dfrac{1}{2}\)
Hai tg AME và tg EMC có đường cao từ C->AD = đường cao từ M->EC nên
\(\dfrac{S_{AME}}{S_{EMC}}=\dfrac{AM}{EC}=\dfrac{1}{2}\)
Hai tg MAB và tg ABC có chung AB nên
\(\dfrac{S_{MAB}}{S_{ABC}}=\) đường cao từ A->AB / đường cao từ C->AB = \(\dfrac{AM}{EC}=\dfrac{1}{2}\)
\(\Rightarrow S_{MAB}=\dfrac{1}{2}xS_{ABC}=\dfrac{1}{2}x\dfrac{1}{4}xS_{ABCD}=\dfrac{1}{8}xS_{ABCD}=2,5cm^2\)