giá trị nhỏ nhất của A=(x.x+2)(x.x+2)+2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



TXĐ: D= [ -3; 1].
Đặt:
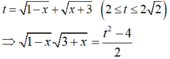
Khi đó phương trình trở thành:
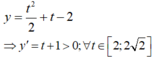
Do đó hàm số đồng biến trên D.
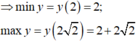
Chọn B.

a)để A max thì 9-x min
do đó : 9-x bé hơn hoặc bằng 0. Mặt khác : A=2016\9-x => 9-x khác 0
do đó : 9-x bé hơn hoặc bằng 1. Mà để A max => 9-x min => 9-x=1=> x=8
Và A max=2016
b) B=x2 -5\x2-2 => B= x2-2-3\x2-2 = 1-3\x2-2
vì 1 là số nguyên => Đê B nguyên thì 3\x2-2 nguyên => x2-2 thuộc ước của 3
sau đó bạn chỉ cần tìm ước của 3 là tìm dk x

a.
\(P=\frac{6}{x^2-6x+17}\)
Ta thấy: $x^2-6x+17=(x-3)^2+8\geq 8$ với mọi $x\in\mathbb{R}$
$\Rightarrow P=\frac{6}{x^2-6x+17}\leq \frac{6}{8}=\frac{3}{4}$
Vậy $P_{\max}=\frac{3}{4}$. Giá trị này đạt tại $x-3=0\Leftrightarrow x=3$
b/
Ta có:
$6=a^2+b^2-ab=\frac{1}{2}(a^2+b^2)+\frac{1}{2}(a^2+b^2-2ab)$
$=\frac{1}{2}(a^2+b^2)+\frac{1}{2}(a-b)^2\geq \frac{1}{2}(a^2+b^2)$ với mọi $a,b$
$\Rightarrow 12\geq a^2+b^2$
Vậy $P_{\max}=12$. Giá trị này đạt tại $a=b=\pm \sqrt{6}$

\(x+y=2\)
\(\Rightarrow x=2-y\)
P= \(x^3+x^2y-2x^2-xy-y^2+3y+x+2017\)
= \(x^3-x^2\left(2-y\right)-y\left(x+y\right)+\left(x+y\right)+2y+2017\)
= \(x^3-x^2.x-2y+2+2y+2017\)
= \(2019\)
Chúc bạn học tốt! ^^

\(\left(x.x+1\right)\left(x-1\right)\left(x.x.x+1\right)=0\)
TH1 : \(x.x+1=0\Leftrightarrow x^2+1=0\Rightarrow x^2=-1\) ( loại )
TH2 : \(x-1=0\Rightarrow x=1\) ( chọn )
TH3 : \(x.x.x+1=0\Leftrightarrow x^3+1=0\Rightarrow x^3=-1\Rightarrow x=-1\) ( chọn )
Vậy có 2 giá trị của x thỏa mãn đề bài