ABCD là hình bình hành EA=ED, FB=FC chứng minh BE=DE và ABE =CDF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 8 2018
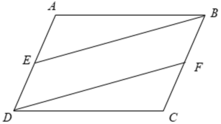
Xét tứ giác BEDF có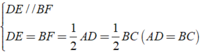
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên
CM
29 tháng 12 2019
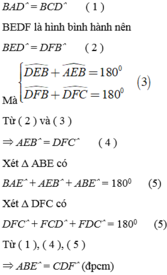
a) Ta chứng minh được BEDF là hình bình hành Þ BE = DF và E B F ^ = C D F ^ .
Cách khác: DAEB = DCFD (c.g.c) suy ra BE = DF và A B E ^ = C D F ^ .
b) Vì BEDF hình bình hành Þ ĐPCM
14 tháng 10 2021
Xét hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB
Xét tứ giác AEFB có EF//BA
nên AEFB là hình thang
mà \(\widehat{A}=\widehat{B}\)
nên AEFB là hình thang cân
14 tháng 10 2021
Trong Hình thang cân ABCD có
AE=BE và BF=CF
\(\Rightarrow\)EF là đường trung bình của hình thang ABCD
\(\Rightarrow\)EF//AB (1) và EF//CD \(\Rightarrow\)\(\widehat{AEF}=\widehat{EDC}\) và \(\widehat{BFE}=\widehat{FCD}\) (so le trong)
Mà \(\widehat{C}=\widehat{D}\) (Hình thang ABCD cân)
\(\Rightarrow\widehat{AEF}=\widehat{BFE}\) (2)
(1),(2) \(\Rightarrow\)Hình thang ABFE cân (đáy AB//FE)
19 tháng 11 2023
Bài 1:
ABCD là hình bình hành
=>AD=BC(1)
E là trung điểm của AD
=>\(EA=ED=\dfrac{AD}{2}\left(2\right)\)
F là trung điểm của BC
=>\(FB=FC=\dfrac{BC}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra EA=ED=FB=FC
Bài 2:
a: ABCD là hình bình hành
=>\(\widehat{A}+\widehat{B}=180^0\)
=>\(\widehat{B}=180^0-60^0=120^0\)
ABCD là hình bình hành
=>\(\widehat{A}=\widehat{C};\widehat{B}=\widehat{D}\)
\(\widehat{A}=\widehat{C}\)
mà \(\widehat{A}=60^0\)
nên \(\widehat{C}=60^0\)
\(\widehat{B}=\widehat{D}\)
mà \(\widehat{B}=120^0\)
nên \(\widehat{D}=120^0\)
b: ABCD là hình bình hành
=>\(\widehat{A}=\widehat{C}\)
mà \(\widehat{A}+\widehat{C}=140^0\)
nên \(\widehat{A}=\widehat{C}=\dfrac{140^0}{2}=70^0\)
ABCD là hình bình hành
=>\(\widehat{A}+\widehat{B}=180^0\)
=>\(\widehat{B}=180^0-70^0=110^0\)
ABCD là hình bình hành
=>\(\widehat{B}=\widehat{D}\)
mà \(\widehat{B}=110^0\)
nên \(\widehat{D}=110^0\)
c: ABCD là hình bình hành
=>\(\widehat{B}+\widehat{A}=180^0\)
mà \(\widehat{B}-\widehat{A}=40^0\)
nên \(\widehat{B}=\dfrac{180^0+40^0}{2}=110^0;\widehat{A}=\dfrac{180^0-40^0}{2}=70^0\)
ABCD là hình bình hành
=>\(\widehat{A}=\widehat{C};\widehat{B}=\widehat{D}\)
=>\(\widehat{C}=70^0;\widehat{D}=110^0\)
22 tháng 3 2020
Bạn tự vẽ hình nhé!
Giải
a) Ta có:
\(\widehat{EAF}+\widehat{EAB}+\widehat{BAD}+\widehat{DAF}=360^0\)
\(\Rightarrow\widehat{EAF}+60^0+60^0+110^0=360^0\)
\(\Rightarrow\widehat{EAF}=130^o\)
b) Vì ABCD là hình bình hành nên:
\(\widehat{BAD}+\widehat{ADC}=180^o\)
\(110^o+\widehat{ADC}=180^o\)
\(\Rightarrow\widehat{ADC}=70^o\)
\(\Rightarrow\widehat{CDF}=\widehat{ADC}+\widehat{ADF}=70^o+60^o=130^o\)
Xét \(\Delta\)EAF và \(\Delta\)CDF có:\(\hept{\begin{cases}AE=DC\left(=AB\right)\\AF=DF\\\widehat{EAF}=\widehat{CDF}=130^o\end{cases}\Rightarrow\Delta EAF=\Delta CDF\left(cgc\right)}\)
c) Ta có: \(\Delta EAF=\Delta CDF\left(cmt\right)\Rightarrow EF=CF\)
Tương tự cũng có: \(\Delta CDF=\Delta EBC\left(cgc\right)\Rightarrow CF=EC\)
\(\Rightarrow\Delta\)EFC là tam giác đều (đpcm)
Xét ΔABE và ΔCDF có
AB=CD
\(\widehat{A}=\widehat{C}\)
AE=CF
Do đó: ΔABE=ΔCDF
Suy ra: \(\widehat{ABE}=\widehat{CDF}\)