Hai bán kính OA, OB của đường tròn (O; R) tạo với nhau một góc 750 thì độ dài cung nhỏ AB là:
A. \(\frac{3\pi R}{4}\)
B. \(\frac{5\pi R}{12}\)
C. \(\frac{7\pi R}{24}\)
D. \(\frac{4\pi R}{5}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
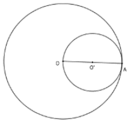
Vì hai đường tròn có một điểm chung là A và 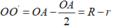 nên hai đường tròn tiếp xúc trong
nên hai đường tròn tiếp xúc trong

Đáp án D
Hai đường tròn có một điểm chung là A nên hai đường tròn tiếp xúc nhau.
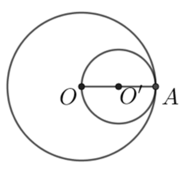


a, 2πR = 4π => R = 2cm
b, A O B ^ = 60 0 (DOAB đều)
=> B O C ^ = 120 0
l B C ⏜ n h ỏ = π . R . 120 180 = 4 π 3 cm
và l B C ⏜ l ớ n = 8 3 π cm

a: Xét ΔBAO vuông tại A có \(cosAOB=\dfrac{OA}{OB}=\dfrac{1}{\sqrt{2}}\)
=>\(\widehat{AOC}=45^0\)
=>\(sđ\left(OA;OC\right)=45^0\)
b: Số đo cung AC nhỏ là:
\(sđ\stackrel\frown{AC}=45^0\)
Số đo cung AC lớn là:
3600-450=3150

Xét ΔOAI và ΔOBI có
OA=OB
OI chung
AI=BI
Do đó: ΔOAI=ΔOBI
Suy ra: \(\widehat{AOI}=\widehat{BOI}\)
hay OI là tia phân giác của góc xOy
\(l_{\stackrel\frown{AB}}=\frac{\pi R.75}{180}=\frac{5\pi R}{12}\)