tìm chu kì của hàm số
f(x)= cos^2 x
f(x)=|cos x|
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Ta có: \(y = \cos x\)
\(y\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = y\)
Suy ra hàm số \(y = \cos x\) là hàm số chẵn
Vậy ta chọn đáp án C
P
2
6 tháng 9 2021
Ta có cos2(x + π) = [-cosx]2 = cos2x
Giả sử tồn tại số T ∈ (0 ; π) thỏa mãn
cos2x = cos2(x + T) với mọi x
⇔ 2cos2x - 1 = 2cos2(x + T) - 1 với mọi x
⇔ cos2x = cos (2x + 2T) với mọi x (1)
(*) : cos2x = cos (2x + 2T)
Thay x = \(\pi\) vào ta được
1 = cos(T + 2π) ⇔ cosT = 1
Do T ∈ (0 ; π) nên cosT ≠ 1.
Vậy x = π không thỏa mãn (*) : cos2x = cos (2x + 2T)
Vậy (1) là mệnh đề sai
Dẫn đến mệnh đề "Giả sử" là sai
Nói cách khác : Không có số T ∈ (0 ; π) thỏa mãn cos2x = cos2(x + T) với mọi x
Tóm lại : T = π là số dương bé nhất thỏa mãn cos2x = cos2(x + T)
nên chu kì của hàm số này là π
AH
Akai Haruma
Giáo viên
6 tháng 9 2021
Lời giải:
$y=f(x)=\cos ^2x=\frac{\cos 2x+1}{2}$
Hàm này có chu kỳ $T=\frac{2\pi}{|2|}=\pi$
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Biểu thức \(\frac{{1 - \cos x}}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)
b) Biểu thức \(\sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} \) có nghĩa khi \(\left\{ {\begin{array}{*{20}{c}}{\frac{{1 + \cos x}}{{2 - \cos x}} \ge 0}\\{2 - \cos x \ne 0}\end{array}} \right.\)
Vì \( - 1 \le \cos x \le 1 ,\forall x \in \mathbb{R}\)
Vậy tập xác định của hàm số là \(D = \mathbb{R}\)
PT
1
CM
25 tháng 1 2018
+ Vẽ đồ thị hàm số y = cos x.
+ Vẽ đường thẳng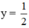 
+ Xác định hoành độ các giao điểm.
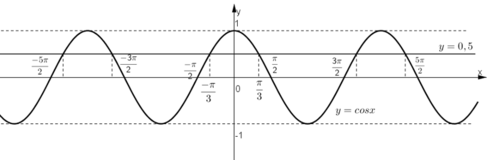
Ta thấy đường thẳng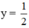 
cắt đồ thị hàm số y = cos x tại các điểm có hoành độ
B
1
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
\(\begin{array}{l}f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\cos x - \cos {x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - 2\,.\,\sin \frac{{x + {x_0}}}{2}.\sin \frac{{x - {x_0}}}{2}}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{ - 2.\frac{{x - {x_0}}}{2}.\sin \frac{{x + {x_0}}}{2}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \,\left( { - \sin \frac{{x + {x_0}}}{2}} \right) = - \sin \frac{{2{x_0}}}{2} = - \sin {x_0}\\ \Rightarrow f'(x) = (\cos x)' = - \sin x\end{array}\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
24.
\(cos\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
\(y_{max}=4\)
26.
\(y=\sqrt{2}cos\left(2x-\dfrac{\pi}{4}\right)\)
Do \(cos\left(2x-\dfrac{\pi}{4}\right)\le1\Rightarrow y\le\sqrt{2}\)
\(y_{max}=\sqrt{2}\)
b.
\(\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\x-\dfrac{\pi}{6}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)