/2x-1/+x = 14
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2019
a/ ĐKXĐ: \(x\ge1\)
Khi \(x\ge1\) ta thấy \(\left\{{}\begin{matrix}VT>0\\VP=1-x\le0\end{matrix}\right.\) nên pt vô nghiệm
b/ \(x\ge1\)
\(\sqrt{\sqrt{x-1}\left(x-2\sqrt{x-1}\right)}+\sqrt{\sqrt{x-1}\left(x+3-4\sqrt{x-1}\right)}=\sqrt{x-1}\)
\(\Leftrightarrow\sqrt{\sqrt{x-1}\left(\sqrt{x-1}-1\right)^2}+\sqrt{\sqrt{x-1}\left(\sqrt{x-1}-2\right)^2}=\sqrt{x-1}\)
Đặt \(\sqrt{x-1}=a\ge0\) ta được:
\(\sqrt{a\left(a-1\right)^2}+\sqrt{a\left(a-2\right)^2}=a\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\Rightarrow x=1\\\sqrt{\left(a-1\right)^2}+\sqrt{\left(a-2\right)^2}=\sqrt{a}\left(1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left|a-1\right|+\left|a-2\right|=\sqrt{a}\)
- Với \(a\ge2\) ta được: \(2a-3=\sqrt{a}\Leftrightarrow2a-\sqrt{a}-3=0\Rightarrow\left[{}\begin{matrix}\sqrt{a}=-1\left(l\right)\\\sqrt{a}=\frac{3}{2}\end{matrix}\right.\)
\(\Rightarrow a=\frac{9}{4}\Rightarrow\sqrt{x-1}=\frac{9}{4}\Rightarrow...\)
- Với \(0\le a\le1\) ta được:
\(1-a+2-a=\sqrt{a}\Leftrightarrow2a+\sqrt{a}-3=0\Rightarrow\left[{}\begin{matrix}a=1\\a=-\frac{3}{2}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x-1}=1\Rightarrow...\)
- Với \(1< a< 2\Rightarrow a-1+2-a=\sqrt{a}\Leftrightarrow a=1\left(l\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2019
c/ ĐKXĐ: \(x\ge\frac{49}{14}\)
\(\Leftrightarrow\sqrt{14x-49+14\sqrt{14x-49}+49}+\sqrt{14x-49-14\sqrt{14x-49}+49}=14\)
\(\Leftrightarrow\sqrt{\left(\sqrt{14x-49}+7\right)^2}+\sqrt{\left(\sqrt{14x-49}-7\right)^2}=14\)
\(\Leftrightarrow\left|\sqrt{14x-49}+7\right|+\left|7-\sqrt{14x-49}\right|=14\)
Mà \(VT\ge\left|\sqrt{14x-49}+7+7-\sqrt{14x-49}\right|=14\)
Nên dấu "=" xảy ra khi và chỉ khi:
\(7-\sqrt{14x-49}\ge0\)
\(\Leftrightarrow14x-49\le49\Leftrightarrow x\le7\)
Vậy nghiệm của pt là \(\frac{49}{14}\le x\le7\)
ND
2
5 tháng 8 2021
Ta có: \(\left(-2x+1\right)\left(x+3\right)+\left(x+1\right)\left(2x-1\right)=14\)
\(\Leftrightarrow-2x^2-6x+x+3+2x^2-x+2x-1=14\)
\(\Leftrightarrow-4x=12\)
hay x=-3
LM
0
13 tháng 6 2023
a: \(=\dfrac{2\left(x+2\right)\left(x-1\right)}{x+2}=2x-2\)
b: \(=\dfrac{2x^3+x^2-6x^2-3x+2x+1}{2x+1}=x^2-3x+1\)
c: \(=\dfrac{x^3+2x^2-2x^2-4x+2x+4}{x+2}=x^2-2x+2\)
d: \(=\dfrac{x^2\left(x-3\right)}{x-3}=x^2\)
L
1
20 tháng 5 2022
a: Đặt |x|=a
Pt trở thành \(3a^2-14a-5=0\)
=>(a-5)(3a+1)=0
=>a=5(nhận) hoặc a=-1/3(loại)
=>x=-5 hoặc x=5
c: \(\left|x+2\right|-2x+1=x^2+2x+3\)
\(\Leftrightarrow\left|x+2\right|=x^2+4x+2\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+4x+2>=0\\\left(x^2+4x+2-x-2\right)\left(x^2+4x+2+x+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left(x^2+3x\right)\left(x^2+5x+4\right)=0\)
hay \(x\in\left\{0;-3;-1;-4\right\}\)
27 tháng 6 2021
b) Ta có: \(\left(x^2-7\right)\left(x+2\right)-\left(2x-1\right)\left(x-14\right)+x\left(x^2-2x-22\right)+35\)
\(=x^3+2x^2-7x-14-\left(2x^2-28x-x+14\right)+x^3-2x^2-22x+35\)
\(=2x^3-29x+21-2x^2+29x-14\)
\(=2x^3-2x^2+7\)
TH
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 12 2022
\(\dfrac{x-14}{x^2-4x}\) - \(\dfrac{3}{2x}\) + \(\dfrac{x+1}{2x-8}\) Đk x #0; x # 4
= \(\dfrac{x-14}{x(x-4)}\) - \(\dfrac{3}{2x}\) + \(\dfrac{x+1}{2(x-4)}\)
= \(\dfrac{2.(x-14)-3.(x-4)+x.(x+1)}{2.x.(x-4)}\)
= \(\dfrac{2x-28-3x+12+x^2+x}{2x(x-4)}\)
= \(\dfrac{x^2-16}{2x(x-4)}\)
= \(\dfrac{(x-4).(x+4)}{2x(x-4)}\)
= \(\dfrac{x+4}{2x}\)
9 tháng 6 2020
a, \(\frac{x}{2x+6}+\frac{x}{2x-2}=\frac{3x+2}{\left(x+1\right)\left(x+3\right)}\) Đkxđ : \(x\ne-1;x\ne-3\)
⇌ x(x + 1) - x(x - 3) = 2(3x + 2)
⇌ x2 + x - x2 - 3x = 6x + 4
⇌ -8x = 4
⇌ x = \(-\frac{1}{2}\) ( tm đk)
→ S = \(\left\{-\frac{1}{2}\right\}\)
b, \(\frac{5}{x+7}+\frac{8}{2x+14}=\frac{2}{3}\) Đkxđ : \(x\ne-7\)
⇌ 30 + 24 = 2(x + 7)
⇌ 2x = 40
⇌ x = 20 (tmđk)
→ S = \(\left\{20\right\}\)
c, \(\frac{x-1}{\frac{x-1}{x+1}}=\frac{2x-1}{x^2+x}\) Đkxđ : \(x\ne-1\)
⇌ x = 2x - 1
⇌ x = 1 (tmđk)
→ S = \(\left\{1\right\}\)
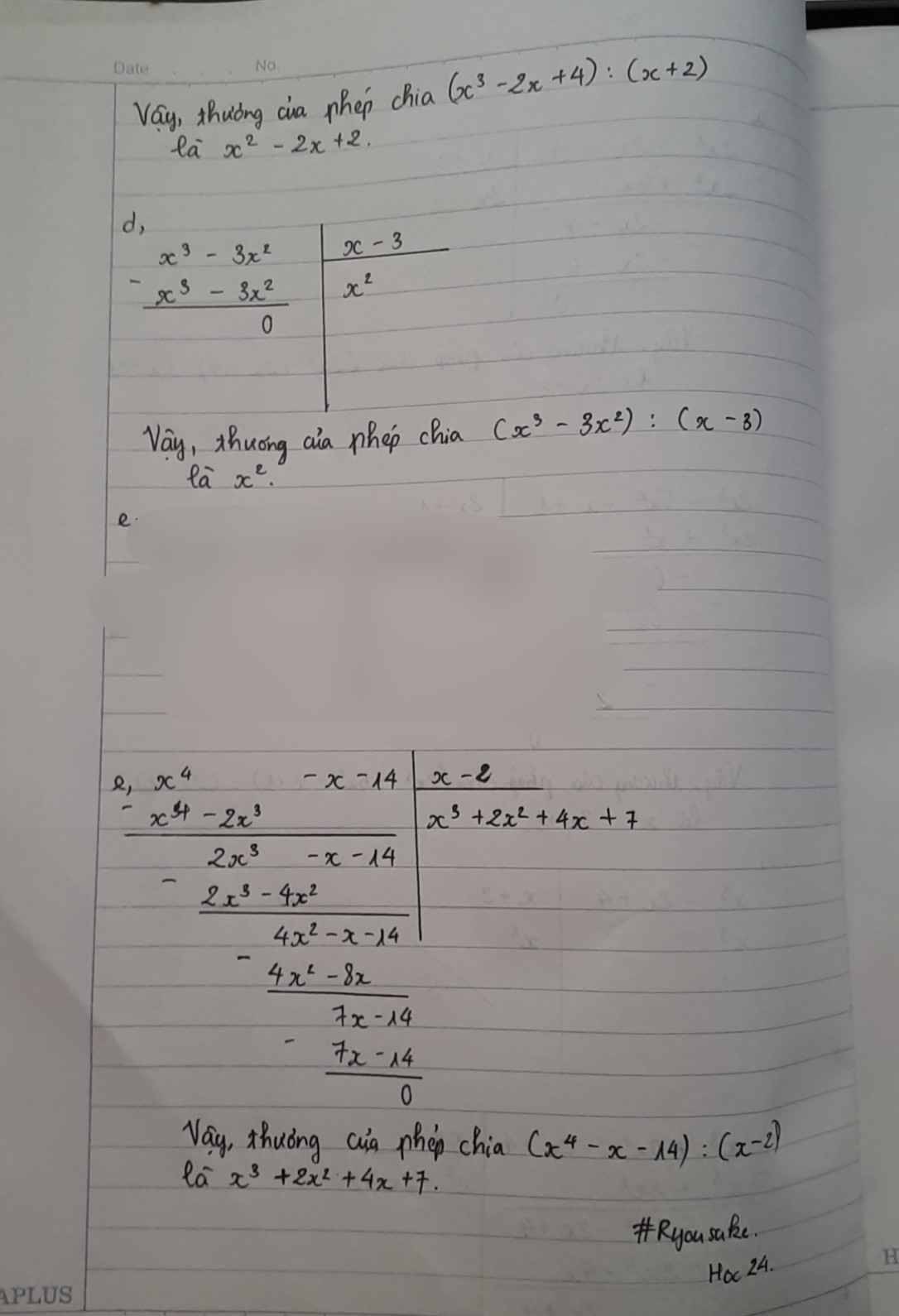
\(\left|2x-1\right|+x=14\)
\(\left|2x-1\right|=2x-1\)khi \(2x-1\ge0\)hay \(x\ge\frac{1}{2}\)
\(\left|2x-1\right|=-\left(2x-1\right)\)khi \(2x-1< 0\)hay \(x< \frac{1}{2}\)
Quy về giải hai phương trình :
\(2x-1+x=14\)( \(x\ge\frac{1}{2}\))
\(\Leftrightarrow3x-1=14\)
\(\Leftrightarrow3x=15\)
\(\Leftrightarrow x=5\)( tmđk )
\(-\left(2x-1\right)+x=14\)( \(x< \frac{1}{2}\))
\(\Leftrightarrow-2x+1+x=14\)
\(\Leftrightarrow-x+1=14\)
\(\Leftrightarrow-x=13\)
\(\Leftrightarrow x=-13\)( tmđk )
Vậy nghiệm của phương trình là S = { 5 ; -13 }
Lắm trò !
\(\left|2x-1\right|+x=14\)
\(\Leftrightarrow\left|2x-1\right|=14-x\)
\(\Leftrightarrow\hept{\begin{cases}2x-1=14-x\\-2x+1=14-x\end{cases}\Leftrightarrow\hept{\begin{cases}3x=15\\-x=13\end{cases}\Leftrightarrow}\hept{\begin{cases}x=5\\x=-13\end{cases}}}\)
Vậy nghiệp pt lần lượt là 5 ; -13