3.22x+1+1/2=49/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 7 2018
Chọn D.
Phương trình 
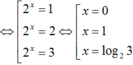thỏa mãn (*)
Do đó S = 1+ log23 = log26.
CM
10 tháng 8 2019
Đáp án D
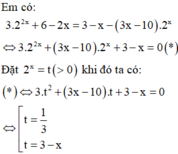
Coi là phương trình bậc hai ẩn t, tính ∆ theo biến em có:
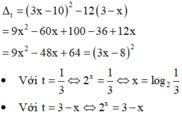
Xét hàm số f x = 2 x đồng biến trên − ∞ ; + ∞ , hàm số g x = 3 − x nghịch biến trên − ∞ ; + ∞
Mà f(1) = g(1) => Phương trình có nghiệm duy nhất x = 1
Vậy phương trình (*) có 2 nghiệm => tổng các nghiệm là
1 + log 2 1 3 = log 2 2 + log 2 1 3 = log 2 2 3
NN
0
DB
1
19 tháng 1 2024
\(A=\left(\dfrac{1}{49}-\dfrac{1}{2^2}\right)\left(\dfrac{1}{49}-\dfrac{1}{3^2}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{100^2}\right)\)
\(=\left(\dfrac{1}{49}-\dfrac{1}{7^2}\right)\left(\dfrac{1}{49}-\dfrac{1}{2^2}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{100^2}\right)\)
\(=\left(\dfrac{1}{49}-\dfrac{1}{49}\right)\left(\dfrac{1}{49}-\dfrac{1}{4}\right)\cdot...\cdot\left(\dfrac{1}{49}-\dfrac{1}{10000}\right)\)
=0
26 tháng 1 2023
So sánh tổng : S = 1/5 + 1/9 + 1/10 + 1/41 + 1/42 với 1/2
NC
26 tháng 1 2023
S=
=50/50+50/49+50/48+...+50/2
=50.(1/50+1/49+1/48+...+1/4+1/3+1/2)
=50
P=
P=(1/49+1)+(2/48+1)+...+(48/2+1)+1
P= 50/49+50/48+....+50/2+50/50=1
vậy s/p = 1/50
VN
0
BB
0
DP
7
14 tháng 5 2015
P = 1/49+2/48+3/47+...+48/2+49/1
Cộng 1 váo mỗi p/s trong 48 p/s đầu , trừ p/s cuối đi 48 ta đượ
P=(1/49+1)+(2/48+1)+...+(48/2+1)+1
P= 50/49+50/48+....+50/2+50/50
Đưa ps cuối lên đầu
P=50/50+50/49+50/48+...+50/2
=50.(1/50+1/49+1/48+...+1/4+1/3+1/2)
=50.S
VậyS/P=1/50
Đề bài: Tìm x
\(3.2^{x+1}+\frac{1}{2}=\frac{49}{2}\)
\(3.2^{x+1}=\frac{49}{2}-\frac{1}{2}\)
\(3.2^{x+1}=24\)
\(2^{x+1}=24\div3\)
\(2^{x+1}=8\)
\(2^{x+1}=2^3\)
\(\Rightarrow x+1=3\)
\(x=2\)
Vậy \(x=2.\)
\(3.2^{2x+1}+\frac{1}{2}=\frac{49}{2}\)
\(\Leftrightarrow3.2^{2x+1}=\frac{48}{2}\)
\(\Leftrightarrow2^{2x+1}=8\)
\(\Leftrightarrow2^{2x+1}=2^3\)
\(\Rightarrow2x+1=3\)
\(\Rightarrow x=1\)