chứng minh rằng ba đường trung bình của tam giác chia tam giác đó thành 4 tam giác bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 2 2021
Gọi AM, BN, CL là các trung tuyến của tam giác ABC => G là trọng tâm của tam giác ABC. Ta cần phải chứng minh S(GAB)=S(GBC)=S(GAC). + Hai tam giác AMC và tam giác ABC có chung đường cao hạ từ A xuống BC nên S(AMC)/S(ABC)=MC/BC=1/2 => S(AMC)=S(ABC)/2 (1) + Hai tam giác GAC và tam giác AMC có chung đường cao hạ từ C xuống AM nên S(GAC)/S(AMC)=AG/AM=2/3 (3 đường trung tuyến cắt nhau tại 1/3 mmỗi đường kể từ đáy) => S(GAC)=2.S(AMC)/3 (2) Từ (1) và (2) => S(GAC)=S(ABC)/3 + Tương tự cũng c/m được S(GAB)=S(GBC)=S(ABC)/3 => Trọng tâm của tam giác khi nối với đỉnh của tam giác ABC thì chia tam giác ABC thành 3 tam giác nhỏ có diện tích bằng nhau
20 tháng 2 2017
Các đường trung tuyến cắt nhau tại trọng tâm
=> vẽ hình ra sẽ nhận thấy 6 tam giác: Tam giác ABC trọng tâm G
Xét 2 tam giác có đáy chung cạnh thì hiển nhiên diện tích bằng nhau do có chung đương cao và đáy bằng nhau => diện tích bằng 1/2 diện tích tam giác đỉnh G đáy là canh tam giác ABC
Xét các tam giác đỉnh G đáy là cạnh của tam giác ABC có 3 tam giác đó có diện tích bằng nhau
Từ 2 điều trên => diện tích 6 tam giác nhỏ đó = nhau
31 tháng 12 2022
Xét ΔABM có AHvừa là đường cao, vừa là phân giác
nên ΔABM cân tại A
=>H là trung điểm của BM
Xét ΔAHC có AM là phân giác
nên AH/AC=CM/MH=CM/2MB=CM/2MC=1/2
Xet ΔAHC vuông tại H có sin ACH=AH/AC=1/2
nên góc ACH=30 độ
=>góc HAC=60 độ
=>góc BAH=1/2*góc HAC=30 độ
=>góc BAC=90 độ
=>ΔABC vuông tại A
Xét ΔABC vuông tại A có góc B+góc C=90 độ
=>góc B=60 độ
mà ΔAMB cân tại A
nên ΔAMB đều
31 tháng 10 2023
Xét ΔABM có AHvừa là đường cao, vừa là phân giác
nên ΔABM cân tại A
=>H là trung điểm của BM
Xét ΔAHC có AM là phân giác
nên AH/AC=CM/MH=CM/2MB=CM/2MC=1/2
Xet ΔAHC vuông tại H có sin ACH=AH/AC=1/2
nên góc ACH=30 độ
=>góc HAC=60 độ
=>góc BAH=1/2*góc HAC=30 độ
=>góc BAC=90 độ
=>ΔABC vuông tại A
Xét ΔABC vuông tại A có góc B+góc C=90 độ
=>góc B=60 độ
mà ΔAMB cân tại A
nên
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
MN là đường trung bình của tam giác ABC
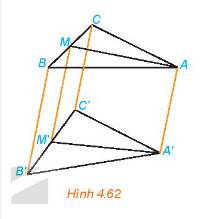
Vì M là trung điểm của BC nên B, M, C thẳng hàng theo thứ tự đó và \(\frac{{BM}}{{MC}} = 1\).
Do vậy, B’, M’, C’ thẳng hàng theo thứ tự đó và \(\frac{{B'M'}}{{M'C'}} = 1\).
Tức M’ là trung điểm của B’C’.
Tương tự, N’ là trung điểm của A’C’.
Vậy M’N’ là đường trung bình của tam giác A’B’C’.
31 tháng 10 2023
Xét ΔABM có AHvừa là đường cao, vừa là phân giác
nên ΔABM cân tại A
=>H là trung điểm của BM
Xét ΔAHC có AM là phân giác
nên AH/AC=CM/MH=CM/2MB=CM/2MC=1/2
Xet ΔAHC vuông tại H có sin ACH=AH/AC=1/2
nên góc ACH=30 độ
=>góc HAC=60 độ
=>góc BAH=1/2*góc HAC=30 độ
=>góc BAC=90 độ
=>ΔABC vuông tại A
Xét ΔABC vuông tại A có góc B+góc C=90 độ
=>góc B=60 độ
mà ΔAMB cân tại A
nên ΔAMB đều
2 tháng 1 2017 lúc 21:06
CM
7 tháng 4 2018
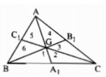
Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6
Chứng minh hoàn toàn tương tự như bài 4.4 ta có
SGAB = SGBC = SGCA = 1/3 SABC
Ta lại có S1 = S2, S3 = S4, S5 = S6 (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau, vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau)
18 tháng 5 2022
Hình vẽ:
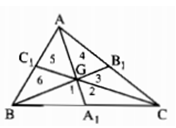
Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6
Vì G là trọng tâm nên ta có:
\(S_{GAB}=S_{GBC}=S_{GCA}=\dfrac{1}{3}S_{ABC}\)
Ta lại có \(S_1=S_2;S_3=S_4;S_5=S_6\) (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau, vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau)
PT
7
28 tháng 6 2016
Gọi AM, BN, CL là các trung tuyến của tam giác ABC
=> G là trọng tâm của tam giác ABC. Ta cần phải chứng minh S(GAB)=S(GBC)=S(GAC).
+ Hai tam giác AMC và tam giác ABC có chung đường cao hạ từ A xuống BC nên
S(AMC)/S(ABC)=MC/BC=1/2 => S(AMC)=S(ABC)/2 (1)
+ Hai tam giác GAC và tam giác AMC có chung đường cao hạ từ C xuống AM nên
S(GAC)/S(AMC)=AG/AM=2/3 (3 đường trung tuyến cắt nhau tại 1/3 mmỗi đường kể từ đáy)
=> S(GAC)=2.S(AMC)/3 (2)
Từ (1) và (2) => S(GAC)=S(ABC)/3
+ Tương tự cũng c/m được
S(GAB)=S(GBC)=S(ABC)/3
=> Trọng tâm của tam giác khi nối với đỉnh của tam giác ABC thì chia tam giác ABC thành 3 tam giác nhỏ có diện tích bằng nhau
28 tháng 6 2016
Bạn đặt tên cho các đỉnh rồi chứng minh các tam giác đó bằng nhau nha
có DF; EF là đường trung bình của tg ABC (gt)
=> DF // AC (đl) và EF // AB (đl)
=> ^AED = ^EDF và ^ADE = ^DEF (slt)
xét tg ADE và tg FED có : ED chung
=> tg ADE = tg FED (c-g-c)
tương tự với các tg còn lại nhé b
ta có MN , MP là đường trung bình của tam giác ABC
\(\Rightarrow MP//AC;NP//AB\)
\(\Rightarrow\widehat{ANM}=\widehat{NMP};\widehat{AMN}=\widehat{MNP}\)
Xét tam giác AMN và tam giác PNM có
cạnh MN chung
Do đó ; tam giác AMN = tam giác PNM [ g.c.g ]
Ta làm tương tự xét 2 cặp tam giác còn lại để rút ra trong một tam giác ba đường trung bình chia tam giác ra làm 4 tam giác bằng nhau
Học tốt nhé